题目内容
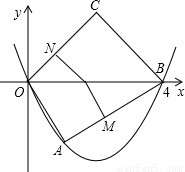
如图,已知一抛物线过坐标原点O和点A(1,h)、B(4,0),C为抛物线对称轴上一点 ,且OA⊥AB,∠COB=45°.
,且OA⊥AB,∠COB=45°.(1)求h的值;
(2)求此抛物线的解析式;
(3)若P为线段OB上一个动点(与端点不重合),过点P作PM⊥AB于M,PN⊥OC于N,试求
| PM |
| OA |
| PN |
| BC |
分析:(1)由OA⊥AB,∠COB=45°可知A(1,h),在Rt△OAB中,由勾股定理得到h;
(2)抛物线与x轴的交点为坐标原点O和B(4,0),故可设此抛物线的解析式为y=ax(x-4),又抛物线过点A(1,-
),解得a;
(3)首先证明∠ONP=∠OCB、和∠PON=∠BOC,进而证明△PON∽△BOC,得到
=
和
=
,两式相加得到所求的式的值.
(2)抛物线与x轴的交点为坐标原点O和B(4,0),故可设此抛物线的解析式为y=ax(x-4),又抛物线过点A(1,-
| 3 |
(3)首先证明∠ONP=∠OCB、和∠PON=∠BOC,进而证明△PON∽△BOC,得到
| PN |
| BC |
| OP |
| OB |
| PM |
| OA |
| PB |
| OB |
解答:解:(1)∵OA⊥AB,A(1,h),在Rt△OAB中,由勾股定理得:(12+h2)+(32+h2)=42,
即h2=3
∵h<0
h=-3
(2)∵抛物线与x轴的交点为坐标原点O和B(4,0),
故可设此抛物线的解析式为y=ax(x-4),
又抛物线过点A(1,-
),
∴-
=a×1×(1-4),
∴a=
故此抛物线的解析式为y=
x(x-4)=
x2-
x,
(3)∵抛物线对称轴垂直平分OB,而C是其上一点,
∴CO=CB,
∴∠COB=∠CBO=45°,
故∠OCB=180°-∠COB-∠CBO=90°.
∵PN⊥OC,
∴∠ONP=90°,
∴∠ONP=∠OCB,
又∠PON=∠BOC,
∴△PON∽△BOC,
∴
=
,
同理可证
=
∴
+
=
+
=1.
即h2=3
∵h<0
h=-3
(2)∵抛物线与x轴的交点为坐标原点O和B(4,0),
故可设此抛物线的解析式为y=ax(x-4),
又抛物线过点A(1,-
| 3 |
∴-
| 3 |
∴a=
| ||
| 3 |
故此抛物线的解析式为y=
| ||
| 3 |
| ||
| 3 |
4
| ||
| 3 |
(3)∵抛物线对称轴垂直平分OB,而C是其上一点,
∴CO=CB,
∴∠COB=∠CBO=45°,
故∠OCB=180°-∠COB-∠CBO=90°.
∵PN⊥OC,
∴∠ONP=90°,
∴∠ONP=∠OCB,
又∠PON=∠BOC,
∴△PON∽△BOC,
∴
| PN |
| BC |
| OP |
| OB |
同理可证
| PM |
| OA |
| PB |
| OB |
∴
| PM |
| OA |
| PN |
| BC |
| PB |
| OB |
| OP |
| OB |
点评:本题主要考查二次函数的应用,求二次函数的解析式等知识点.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 如图,已知一条抛物线C1:
如图,已知一条抛物线C1: (2011•利川市一模)如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0).
(2011•利川市一模)如图,已知:抛物线y=ax2+bx-4(a≠0)与x轴交于A、B两点,与y轴交于点C,A、B两点的坐标分别为A(-6,0)、B(2,0).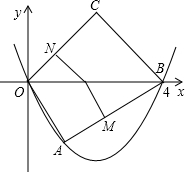 ,且OA⊥AB,∠COB=45°.
,且OA⊥AB,∠COB=45°.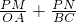 的值.
的值.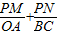 的值.
的值.