题目内容
13.(1)计算:|$\frac{1}{3}$-$\sqrt{3}$|+$\sqrt{2}$sin45°+tan60°-(1-$\frac{1}{3}$)-1-$\sqrt{12}$+(π-3)0.(2)解不等式组:$\left\{\begin{array}{l}{2x-5>0\\①}\\{2-x>-1\\②}\end{array}\right.$.
分析 (1)分别根据绝对值的性质、特殊角的三角函数值、0指数幂及负整数指数幂的计算法则分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)原式=$\sqrt{3}$-$\frac{1}{3}$+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$+$\sqrt{3}$-$\frac{3}{2}$-2$\sqrt{3}$+1
=$\sqrt{3}$-$\frac{1}{3}$+1+$\sqrt{3}$-$\frac{3}{2}$-2$\sqrt{3}$+1
=-$\frac{1}{3}$-$\frac{1}{2}$
=-$\frac{5}{6}$;
(2)由①得,x>$\frac{5}{2}$,
由②得,x<3,
故不等式组的解集为:$\frac{5}{2}$<x<3.
点评 本题考查的是实数的运算,熟知绝对值的性质、特殊角的三角函数值、0指数幂及负整数指数幂的计算法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.一只蚂蚁沿数轴从点A向右直爬15个单位到达点B,点B表示的数为-2,则点A所表示的数为( )
| A. | 15 | B. | 13 | C. | -13 | D. | -17 |
18.下列调查中,适合采用全面调查(普查)方式的是( )
| A. | 了解一批节能灯泡的使用寿命 | |
| B. | 了解某班同学“跳绳”的成绩 | |
| C. | 了解全国每天丢弃的塑料袋的数量 | |
| D. | 了解上海卫视“今晚80后”栏目的收视率 |





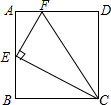 如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论正确的是( )
如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论正确的是( )