题目内容
(2000•绵阳)已知两圆的半径r和R满足 =0,两圆的圆心距d满足(d-5)≠1,那么这两圆的公切线有且只有( )
=0,两圆的圆心距d满足(d-5)≠1,那么这两圆的公切线有且只有( )A.1条
B.2条
C.3条
D.4条
【答案】分析:先根据非负数的性质,零指数幂的计算法则分别求出两圆的半径r和R,两圆的圆心距d,再根据两圆位置关系与数量关系间的联系确定两圆的位置关系,依此得出两圆的公切线的条数.
解答:解:∵ =0,(d-5)≠1,
=0,(d-5)≠1,
∴r2-6r+9=0,解得r=3;
R-7=0,解得R=7;
d-5=0,解得d=5.
∴R+r=10,R-r=4,
得4<5<10,即R-r<d<R+r.
∴两圆相交.
∴这两圆的公切线有且只有2条.
故选B.
点评:本题难度中等,主要考查了非负数的性质,零指数幂,圆与圆的位置关系与数量关系间的联系及公切线的定义.
此类题为中考热点,需重点掌握.
解答:解:∵
 =0,(d-5)≠1,
=0,(d-5)≠1,∴r2-6r+9=0,解得r=3;
R-7=0,解得R=7;
d-5=0,解得d=5.
∴R+r=10,R-r=4,
得4<5<10,即R-r<d<R+r.
∴两圆相交.
∴这两圆的公切线有且只有2条.
故选B.
点评:本题难度中等,主要考查了非负数的性质,零指数幂,圆与圆的位置关系与数量关系间的联系及公切线的定义.
此类题为中考热点,需重点掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
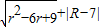 =0,两圆的圆心距d满足(d-5)≠1,那么这两圆的公切线有且只有( )
=0,两圆的圆心距d满足(d-5)≠1,那么这两圆的公切线有且只有( ) .
.
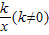 的图象过点P(2,
的图象过点P(2, ),则化简(x-
),则化简(x- )(y+
)(y+ )的结果是( )
)的结果是( )