题目内容
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是( )
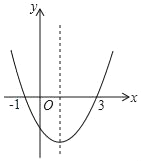
A. a<0 B. c>0
C. a+b+c>0 D. 方程 ax2+bx+c=0的两根是x1=﹣1,x2=3
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是( )

A. a<0 B. c>0
C. a+b+c>0 D. 方程 ax2+bx+c=0的两根是x1=﹣1,x2=3
 阅读快车系列答案
阅读快车系列答案