题目内容
在△ABC中，若
+（1-tanB）2=0，求∠C的度数．
| 2cosA-1 |
分析：根据非负数的性质可得出coaA及tanB的值，继而可得出A和B的度数，根据三角形的内角和定理可得出∠C的度数．
解答：解：由题意，得 cosA=
，tanB=1，
∴∠A=60°，∠B=45°，
∴∠C=180°-∠A-∠B=180°-60°-45°=75°．
| 1 |
| 2 |
∴∠A=60°，∠B=45°，
∴∠C=180°-∠A-∠B=180°-60°-45°=75°．
点评：此题考查了特殊角的三角形函数值及算术平方根及偶次方的非负性，属于基础题，关键是熟记一些特殊角的三角形函数值，也要注意运用三角形的内角和定理．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，∠A、∠B、∠C的对边分别是a、b、c，若∠A：∠B：∠C=1：2：3．则a：b：c=（ ）
A、1：
| ||
B、
| ||
| C、1：1：2 | ||
| D、1：2：3 |
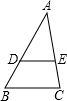如图，在△ABC中，DE∥BC，DE分别与AB、AC相交于点D、E，若AD=4，DB=2，则AE：EC的值为（ ）| A、0.5 | ||
| B、2 | ||
C、
| ||
D、
|