Ő‚ńŅńŕ»›
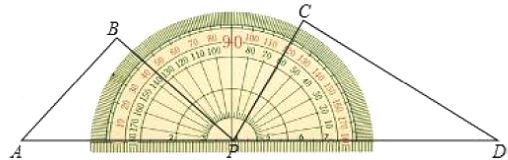
°ĺŐ‚ńŅ°Ņ“ĽłĪ»żĹ«≥Ŗ(∑÷Īūļ¨45°„£¨45°„£¨90°„ļÕ30°„£¨60°„£¨90°„)įī»ÁÕľňý ĺįŕ∑Ň‘ŕŃŅĹ«∆ų…Ō£¨ĪŖPD”ŽŃŅĹ«∆ų0°„ŅŐ∂»ŌŖ÷ōļŌ£¨ĪŖAP”ŽŃŅĹ«∆ų180°„ŅŐ∂»ŌŖ÷ōļŌ£¨Ĺ껿ū≥ŖABP»∆ŃŅĹ«∆ų÷––ńĶ„P“‘√Ņ√Ž10°„ĶńňŔ∂»ň≥ Ī’Ž–ż◊™£¨ĶĪĪŖPB”Ž0°„ŅŐ∂»ŌŖ÷ōļŌ ĪÕ£÷Ļ‘ň∂Į£¨…Ť»żĹ«≥ŖABPĶń‘ň∂Į Īľšő™t.
£®1£©ĶĪt=5 Ī£¨ĪŖPBĺ≠ĻżĶńŃŅĹ«∆ųŅŐ∂»ŌŖ∂‘”¶Ķń∂» ż « ∂»£ļ
£®2£©»Ű‘໿ū≥ŖABPŅ™ ľ–ż◊™ĶńÕ¨ Ī£¨»żĹ«≥ŖPCD“≤»∆Ķ„P“‘√Ņ√Ž2°„ĶńňŔ∂»ńś Ī’Ž–ż◊™£¨ĶĪ»żĹ«≥ŖABPÕ£÷Ļ–ż◊™ Ī£¨»żĹ«≥ŖPCD“≤Õ£÷Ļ–ż◊™.
ĘŔĶĪtő™ļő÷Ķ Ī£¨ĪŖPB∆Ĺ∑÷°ŌCPD£Ľ
Ęŕ‘ŕ–ż◊™Ļż≥Ő÷–£¨ «∑Ůīś‘ŕń≥“Ľ ĪŅŐ Ļ°ŌBPD=2°ŌAPC£¨»Űīś‘ŕ£¨«Ž÷ĪĹ”–ī≥ŲtĶń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”….
°ĺīūįł°Ņ£®1£©![]() £Ľ£®2£©ĘŔ
£Ľ£®2£©ĘŔ![]() √Ž£ĽĘŕ
√Ž£ĽĘŕ![]() √Ž
√Ž
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›–ż◊™Ķń–‘÷ ľīŅ…ľ∆ň„Ķ√≥ŲĹŠ¬Ř£Ľ
£®2£©”…–ż◊™÷™£¨![]() Ķń–ż◊™Ĺ«ő™
Ķń–ż◊™Ĺ«ő™![]() £¨
£¨![]() Ķń–ż◊™Ĺ«ő™
Ķń–ż◊™Ĺ«ő™![]() £¨
£¨
ĘŔłýĺ›PB∆Ĺ∑÷°ŌCPDļÕ∆ĹĹ«Ķń∂®“ŚŃ–≥Ų∑Ĺ≥ŐľīŅ…ľ∆ň„Ķ√≥Ų£Ľ
Ęŕ∑÷PA‘ŕPC◊ů≤ŗļÕ”“≤ŗŃĹ÷÷«ťŅŲĪŪ ĺ≥Ų![]() £¨łý囓—÷™Ĺ®ŃĘ∑Ĺ≥ŐľīŅ…Ĺ‚Ķ√ĹŠ¬Ř.
£¨łý囓—÷™Ĺ®ŃĘ∑Ĺ≥ŐľīŅ…Ĺ‚Ķ√ĹŠ¬Ř.
£®1£©ĶĪ![]() √Ž Ī£¨
√Ž Ī£¨![]() –ż◊™Ńň£ļ
–ż◊™Ńň£ļ![]()
°Ŗ![]() «Ķ»—Ł÷ĪĹ«»żĹ«–ő£¨°ŗ
«Ķ»—Ł÷ĪĹ«»żĹ«–ő£¨°ŗ![]() £¨
£¨
īň Ī£¨ĪŖ![]() ĺ≠ĻżĶńŃŅĹ«∆ųŅŐ∂»ŌŖ∂‘”¶Ķń∂» ż «£ļ
ĺ≠ĻżĶńŃŅĹ«∆ųŅŐ∂»ŌŖ∂‘”¶Ķń∂» ż «£ļ![]() ĽÚ
ĽÚ![]()
°ŗĪŖ![]() ĺ≠ĻżĶńŃŅĹ«∆ųŅŐ∂»ŌŖ∂‘”¶Ķń∂» ż «£ļ
ĺ≠ĻżĶńŃŅĹ«∆ųŅŐ∂»ŌŖ∂‘”¶Ķń∂» ż «£ļ![]()
£®2£©ĘŔ”…–ż◊™÷™£¨![]() Ķń–ż◊™Ĺ«ő™
Ķń–ż◊™Ĺ«ő™![]() £¨
£¨![]() Ķń–ż◊™Ĺ«ő™
Ķń–ż◊™Ĺ«ő™![]() £¨
£¨
°ŗĪŖ![]() –ż◊™ĶńĹ«∂»ő™£ļ
–ż◊™ĶńĹ«∂»ő™£ļ![]() £ĽĪŖ
£ĽĪŖ![]() –ż◊™ĶńĹ«∂»ő™£ļ
–ż◊™ĶńĹ«∂»ő™£ļ![]() £Ľ
£Ľ
°ŗ“ņŐ‚“‚Ķ√£ļ![]() £¨ľī£ļ
£¨ľī£ļ![]()
°ŗ![]() √Ž£Ľ
√Ž£Ľ
ĘŕĶĪPA‘ŕPC◊ů≤ŗ Ī£¨”…–ż◊™÷™£ļ
![]()
![]()
łýĺ›Ő‚“‚£ļ°ŌBPD=2°ŌAPC£¨
Ķ√£ļ![]() £¨ľī£ļ
£¨ľī£ļ![]()
°ŗ![]() √Ž£Ľ
√Ž£Ľ
ĶĪPA‘ŕPC”“≤ŗ Ī£¨”…–ż◊™÷™£ļ
![]()
![]()
łýĺ›Ő‚“‚£ļ°ŌBPD=2°ŌAPC£¨
Ķ√£ļ![]() £¨ľī£ļ
£¨ľī£ļ![]()
°ŗ![]() √Ž£Ľ
√Ž£Ľ
◊Ř…Ō£ļ![]() √Ž£¨°ŌBPD=2°ŌAPC
√Ž£¨°ŌBPD=2°ŌAPC

 Ňŗ”Ňļ√ĺŪĶ•‘™ľ”∆ŕń©ĺŪŌĶŃ–īūįł
Ňŗ”Ňļ√ĺŪĶ•‘™ľ”∆ŕń©ĺŪŌĶŃ–īūįł “ĽŌŖ√Ż ¶»®ÕĢ◊ų“ĶĪĺŌĶŃ–īūįł
“ĽŌŖ√Ż ¶»®ÕĢ◊ų“ĶĪĺŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņń≥≥¨ –ľ∆ĽģĻļĹÝľ◊°Ę““ŃĹ÷÷–ÕļŇĶńĹŕń‹Ķ∆Ļ≤1000÷Ľ£¨’‚ŃĹ÷÷Ĺŕń‹Ķ∆ĶńĹÝľŘ°Ę ŘľŘ»ÁŌ¬ĪŪ£ļ
ĹÝľŘ£®‘™/÷Ľ£© | ŘľŘ£®‘™/÷Ľ£© | |
ľ◊–Õ | 25 | 30 |
““–Õ | 45 | 60 |
£®1£©»ÁĻŻĹÝĽűŅÓ«°ļ√ő™37000‘™£¨ń«√īŅ…“‘ĻļĹÝľ◊–ÕĹŕń‹Ķ∆∂ŗ…Ŕ÷Ľ£Ņ
£®2£©≥¨ –ő™«ž◊£‘™Ķ©ĹÝ––īůīŔŌķĽÓ∂Į£¨ĺŲ∂®∂‘““–ÕĹŕń‹Ķ∆ĹÝ––īÚ’ŘŌķ Ř£¨“™«ů»ę≤Ņ ŘÕÍļů£¨““–ÕĹŕń‹Ķ∆ĶńņŻ»ů¬ ő™20%£¨«Žő ““–ÕĹŕń‹Ķ∆–ŤīÚľł’Ř£Ņ