题目内容
【题目】计算：（1）分解因式：m2（x﹣y）+4n2（y﹣x）；
（2）解不等式组
，并把解集在数轴上表示出来；
（3）先化简，再求解， 
，其中x＝
﹣2.
【答案】（1）（x﹣y）（m＋2n）（m－2n）；（2）
，见解析；（3）4
－6.
【解析】
（1）先提公因式，再用平方差公式二次分解；
（2）先分别解两个不等式，求出它们的解集，再求两个不等式解集的公共部分即可得到不等式组的解集，然后画数轴表示即可；
（3）先把括号内通分化简，然后把分子、分母分解因式约分，再把x＝﹣2代入化简的结果计算.
解：（1）m2（x﹣y）+4n2（y﹣x）
＝（x﹣y）（m2－4n2）
＝（x﹣y）（m＋2n）（m－2n）.
（2）∵
∴
，
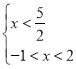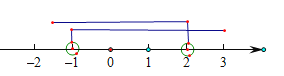
解得：，如下图，
（3）原式＝
＝
＝
，
当x＝﹣2时，原式＝4－6
练习册系列答案
相关题目
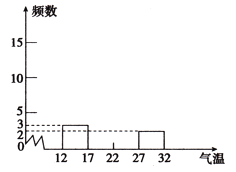
【题目】银川市2019年5月1日---20日的气温（单位：℃）如下：
22 31 25 15 18 23 21 20 27 17
20 12 18 21 21 16 20 24 26 19
解答下列问题：
（1）将下表补充完整：
气温分组 | 12≤x<17 | 17≤x<22 | 22≤x<27 | 27≤x<32 |
频数 | 3 | 2 | ||
百分比 | 15% | 25% |
（2）补全频数直方图
