题目内容
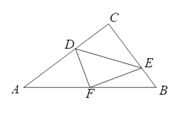
【题目】如图，在△ABC中，∠ACB=90°，点D,E分别在AC,BC上，且∠CDE=∠B，将△CDE 沿DE折叠，点C恰好落在AB边上的点F处，若AC=8,AB=10，则CD的长为____．
【答案】
【解析】分析：由对称性可知CF⊥DE，可得∠CDE=∠ECF=∠B，得出CF=BF，同理可得CF=AF，由此可得F是AB的中点，求得CF=5，再判定△CDF∽△CFA，得到CF2=CD×CA，进而得出CD的长．
详解：
由对称性可知CF⊥DE，
又∵∠DCE=90°，
∴∠CDE=∠ECF=∠B，
∴CF=BF，
同理可得CF=AF，
∴F是AB的中点，
∴CF=
AB=5，
又∵∠DFC=∠ACF=∠A，∠DCF=∠FCA，
∴△CDF∽△CFA，
∴CF2=CD×CA，即52=CD×8，
∴CD=.
故答案是：.
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
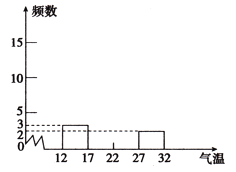
【题目】银川市2019年5月1日---20日的气温（单位：℃）如下：
22 31 25 15 18 23 21 20 27 17
20 12 18 21 21 16 20 24 26 19
解答下列问题：
（1）将下表补充完整：
气温分组 | 12≤x<17 | 17≤x<22 | 22≤x<27 | 27≤x<32 |
频数 | 3 | 2 | ||
百分比 | 15% | 25% |
（2）补全频数直方图
