题目内容
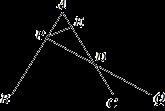
如图，△ABC中，D、E两点分别在AC、BC上，则AB=AC，CD=DE．若∠A=40°，∠ABD：∠DBC=3：4，则∠BDE=（ ）
A．25° B．30° C．35° D．40°
B
【解析】
根据已知及等腰三角形的性质可求得两底角的度数，再根据∠ABD：∠DBC=3：4，列方程求解即可求出∠BDE的度数．
【解析】
∵AB=AC，CD=DE
∴∠C=∠DEC=∠ABC
∴AB∥DE
∵∠A=40°
∴∠C=∠DEC=∠ABC=
=70°
∵∠ABD：∠DBC=3：4
∴设∠ABD为3x，∠DBC为4x
∴3x+4x=70°
∴x=10°
∵AB∥DE
∴∠BDE=∠ABD=30°
故选B．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
B．
C．
D．不能确定
