题目内容
如图,一架飞机以200米/秒的速度由A向B沿水平直线方向飞行,在航线AB的正下方有两个山头C、D.飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°.飞机飞行了半分钟后到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.求山头C、D之间的距离.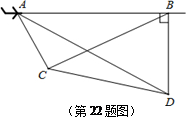

∵飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°
到B处时,往后测得山头C的俯角为30°
∴∠BAC=60°,∠ABC=30°,∠BAD=30°
∴∠ACB=180°-∠ABC-∠BAC=180°-30°-60°=90° 2分
∵AB=200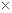 30=6000米
30=6000米
 ∴BC=AB•cos30°=6×
∴BC=AB•cos30°=6×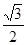 =
=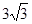
Rt△ABD中,BD=AB•tan30°=6×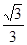 =
=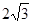 千米 千米
千米 千米
作CE⊥BD于E点,
∵AB⊥BD,∠ABC=30°,∴∠CBE=60° 1分
则BE=BC•cos60°=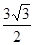 ,DE=BD-BE=
,DE=BD-BE=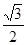 ,CE=BC•sin60°=
,CE=BC•sin60°=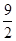 2分
2分
∴CD=DE2+CE2=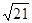 千米
千米
∴山头C、D之间的距离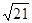 千米. 1分
千米. 1分
到B处时,往后测得山头C的俯角为30°
∴∠BAC=60°,∠ABC=30°,∠BAD=30°
∴∠ACB=180°-∠ABC-∠BAC=180°-30°-60°=90° 2分
∵AB=200
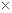 30=6000米
30=6000米  ∴BC=AB•cos30°=6×
∴BC=AB•cos30°=6×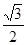 =
=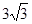
Rt△ABD中,BD=AB•tan30°=6×
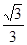 =
=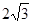 千米 千米
千米 千米 作CE⊥BD于E点,
∵AB⊥BD,∠ABC=30°,∴∠CBE=60° 1分
则BE=BC•cos60°=
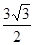 ,DE=BD-BE=
,DE=BD-BE=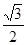 ,CE=BC•sin60°=
,CE=BC•sin60°=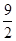 2分
2分∴CD=DE2+CE2=
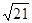 千米
千米∴山头C、D之间的距离
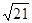 千米. 1分
千米. 1分根据题目中的俯角可以求出∠BAC=60°,∠ABC=30°,∠BAD=30°,进而得到∠ACB=90°,利用AB=6千米求得BC的长,然后求得CD两点间的水平距离,进而求得C、D之间的距离

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
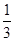 ,AC=3,则AB= .
,AC=3,则AB= .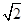 ≈1.414,
≈1.414,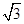 ≈1.732.最后结果精确到1米)
≈1.732.最后结果精确到1米)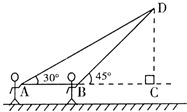
 ABCD中,AB=6,AD=8,∠B=60°,∠BAD与∠CDA的角平分线AE、BF相交于点G,且交BC于点E、F,则图中阴影部分的面积是 。
ABCD中,AB=6,AD=8,∠B=60°,∠BAD与∠CDA的角平分线AE、BF相交于点G,且交BC于点E、F,则图中阴影部分的面积是 。 
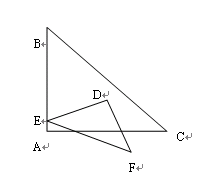
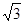 ︰2 B. 1︰3 C. 2︰3 D.
︰2 B. 1︰3 C. 2︰3 D. 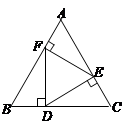
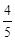 ,则坡面AC的长度为( )
,则坡面AC的长度为( )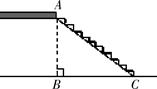
 的补角是120°,则tanA= ▲ 。
的补角是120°,则tanA= ▲ 。