计算或化简:(1)(-12)-2+(-2)3×(-2013)0, 2- 题目和参考答案——青夏教育精英家教网—

题目内容

计算或化简：
（1）(-

)-2+(-2)3×(-2013)0；
（2）（a+3）²-（a-2）（a+2）

考点：完全平方公式,平方差公式,零指数幂,负整数指数幂

专题：

分析：（1）根据x的0次幂等于1即可化简；
（2）首先根据完全平方公式（x-y）²=（x+y）（x-y）即可化简该式，即可解题．

解答：解：（1）(-

)-2+（-2）³×（-2013）⁰
=4+（-8）×1
=4-8
=-4；

（2）（a+3）²-（a-2）（a+2）
=a²+6a+9-（a²-4）
=a²+6a+9-a²+4
=6a+13．

点评：本题考查了平方差公式的运用，考查了x的零次幂等于1的性质，考查了完全平方公式的计算．

练习册系列答案

相关题目

如图，△ABC内接于⊙O，AD是⊙O的直径，∠DAC=62°，则∠ABC=

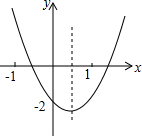二次函数y=ax²+bx+c的图象如图所示，则下列结论①abc＜0，②b²-4ac＞0，③2a+b＞0，④a+b+c＜0，⑤ax²+bx+c+2=0的解为x=-0，其中正确的有（　　）个．

给出下列几何图形：①两个圆；②两个正方形；③两个矩形；④两个正六边形；⑤两个等边三角形；⑥两个直角三角形；⑦两个菱形．其中，一定相似的有

（填序号）．

已知一矩形的两边长分别为10cm和15cm，其中一个内角的平分线分长边为两部分，这两部分的长为（　　）

若（x+3）•（x-p）=x²+mx+36，则p、m的值分别是（　　）

已知：|a|=2，b²=9，ab＜0，求a-b的值．

试题分类