题目内容
15. 如图,在扇形OAB中,∠AOB=90°,半径OA=2$\sqrt{3}$,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则阴影部分的面积是3π-4$\sqrt{3}$.
如图,在扇形OAB中,∠AOB=90°,半径OA=2$\sqrt{3}$,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则阴影部分的面积是3π-4$\sqrt{3}$.
分析 连接OD交BC于点E,由翻折的性质可知:OE=DE=$\sqrt{3}$,在Rt△OBE中,根据特殊锐角三角函数值可知∠OBC=30°,然后在Rt△COB中,可求得CO,从而可求得△COB的面积,最后根据阴影部分的面积=扇形面积-2倍的△COB的面积求解即可.
解答 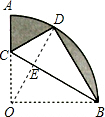 解:连接OD交BC于点E.
解:连接OD交BC于点E.
∴扇形的面积=$\frac{1}{4}$×(2$\sqrt{3}$)2π=3π,
∵点O与点D关于BC对称,
∴OE=ED=$\sqrt{3}$,OD⊥BC.
在Rt△OBE中,sin∠OBE=$\frac{OE}{OB}$=$\frac{1}{2}$,
∴∠OBC=30°.
在Rt△COB中,$\frac{OC}{OB}$=tan30°,
∴$\frac{OC}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
∴CO=2.
∴△COB的面积=$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$.
阴影部分的面积=扇形面积-2倍的△COB的面积
=3π-4$\sqrt{3}$.
故答案为:3π-4$\sqrt{3}$.
点评 本题主要考查的是翻折的性质,扇形面积的计算以及特殊锐角三角函数值的应用,根据翻折的性质求得OE的长,然后再求得∠OBC的度数是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.在平面直角坐标系中,将抛物线C1:y=x2平移后得到抛物线C2,使得抛物线C2恰好经过抛物线C1的顶点,且抛物线C2与x轴有两个交点,分别记为点A、点B.若AB=2$\sqrt{3}$,抛物线C2的顶点为点C,则△ABC的周长是( )
| A. | 3+2$\sqrt{2}$ | B. | 6+2$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
4. 如图是某游乐城的平面示意图,如图用(8,2)表示入口处的位置,用(6,-1)表示球幕电影的位置,那么坐标原点表示的位置是( )
如图是某游乐城的平面示意图,如图用(8,2)表示入口处的位置,用(6,-1)表示球幕电影的位置,那么坐标原点表示的位置是( )
 如图是某游乐城的平面示意图,如图用(8,2)表示入口处的位置,用(6,-1)表示球幕电影的位置,那么坐标原点表示的位置是( )
如图是某游乐城的平面示意图,如图用(8,2)表示入口处的位置,用(6,-1)表示球幕电影的位置,那么坐标原点表示的位置是( )| A. | 太空秋千 | B. | 梦幻艺馆 | C. | 海底世界 | D. | 激光战车 |