题目内容
 直角三角形ABC中∠A=90°,正方形EFGH的四个顶点在三角形的边上,如图.已知BE=6,FC=2,则正方形EFGH的面积是
直角三角形ABC中∠A=90°,正方形EFGH的四个顶点在三角形的边上,如图.已知BE=6,FC=2,则正方形EFGH的面积是
- A.12
- B.16
- C.2

- D.4

A
分析:设正方形HEFG的边长为a,由∠A=90°,方形EFGH的四个顶点在三角形的边上,通过等角的余角相等可得∠BHE=∠C,于是
Rt△BEH∽Rt△GFC,则a:6=2:a,即可得到方形EFGH的面积.
解答:设正方形HEFG的边长为a,
∵∠A=90°,正方形EFGH的四个顶点在三角形的边上,
∴∠B+∠C=90°,
而∠B+∠BHE=90°,
∴Rt△BEH∽Rt△GFC,
∴a:6=2:a,
∴a2=12,
即方形EFGH的面积为12.
故选A.
点评:本题考查了有一个锐角对应相等的两个直角三角形相似以及相似三角形的性质.也考查了正方形的性质.
分析:设正方形HEFG的边长为a,由∠A=90°,方形EFGH的四个顶点在三角形的边上,通过等角的余角相等可得∠BHE=∠C,于是
Rt△BEH∽Rt△GFC,则a:6=2:a,即可得到方形EFGH的面积.
解答:设正方形HEFG的边长为a,
∵∠A=90°,正方形EFGH的四个顶点在三角形的边上,
∴∠B+∠C=90°,
而∠B+∠BHE=90°,
∴Rt△BEH∽Rt△GFC,
∴a:6=2:a,
∴a2=12,
即方形EFGH的面积为12.
故选A.
点评:本题考查了有一个锐角对应相等的两个直角三角形相似以及相似三角形的性质.也考查了正方形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
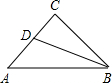 如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=
如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA= 如图,在直角三角形ABC中,∠C=90°,AB=5,AC=3.点P、Q分别是BC边和AB边上的动点,点P从点C向点B运动,点Q从点A向点B运动,QR⊥BC,垂足为R,设P、Q同时运动,并且当P运动4x单位长度时,Q运动5(1-x)单位长度.是否存在x的值,使以P、Q、R为顶点的三角形与△ACP相似?若存在,求出所有x的值;若不存在,说明理由.
如图,在直角三角形ABC中,∠C=90°,AB=5,AC=3.点P、Q分别是BC边和AB边上的动点,点P从点C向点B运动,点Q从点A向点B运动,QR⊥BC,垂足为R,设P、Q同时运动,并且当P运动4x单位长度时,Q运动5(1-x)单位长度.是否存在x的值,使以P、Q、R为顶点的三角形与△ACP相似?若存在,求出所有x的值;若不存在,说明理由. 如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M.
如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M. 如图,直角三角形ABC中,∠ABC=90°,点D、E分别是AC、BC的中点,AB=3,BC=4,则DE和BD的长分别为( )
如图,直角三角形ABC中,∠ABC=90°,点D、E分别是AC、BC的中点,AB=3,BC=4,则DE和BD的长分别为( )