题目内容
 如图,在直角三角形ABC中,∠C=90°,AB=5,AC=3.点P、Q分别是BC边和AB边上的动点,点P从点C向点B运动,点Q从点A向点B运动,QR⊥BC,垂足为R,设P、Q同时运动,并且当P运动4x单位长度时,Q运动5(1-x)单位长度.是否存在x的值,使以P、Q、R为顶点的三角形与△ACP相似?若存在,求出所有x的值;若不存在,说明理由.
如图,在直角三角形ABC中,∠C=90°,AB=5,AC=3.点P、Q分别是BC边和AB边上的动点,点P从点C向点B运动,点Q从点A向点B运动,QR⊥BC,垂足为R,设P、Q同时运动,并且当P运动4x单位长度时,Q运动5(1-x)单位长度.是否存在x的值,使以P、Q、R为顶点的三角形与△ACP相似?若存在,求出所有x的值;若不存在,说明理由.
分析:根据相似三角形的判定与性质,当若点P,R,Q分别与点P,C,A对应,当若点P,R,Q分别与点A,C,P对应,分别分析得出x的长度即可.
解答:解:存在x的值,使以P,Q,R为顶点的三角形与△ACP相似.
∵BQ=5x,有相似三角形求得:BR=4x,QR=3x,
①当P在C,R之间时,PR=4-8x,
若△PRQ∽△ACP,则PR:AC=RQ:CP,
即:
=
,
∴x=
,
若△QRP∽△ACP,则QR:AC=RP:CP,
即:
=
,
∴x1=
-1,x2=-
-1(舍),
②当P在B,R之间时,PR=8x-4,
若△PRQ∽△ACP,则PR:AC=RQ:CP,
即:
=
,
∴x=
,
若△QRP∽△ACP,则QR:AC=RP:CP,
即:
=
,
∴x1=x2=1(舍)
综上所述:存在x的值,x1=
-1,x2=
,x3=
.
∵BQ=5x,有相似三角形求得:BR=4x,QR=3x,
①当P在C,R之间时,PR=4-8x,
若△PRQ∽△ACP,则PR:AC=RQ:CP,
即:
| 4-8x |
| 3 |
| 3x |
| 4x |
∴x=
| 7 |
| 32 |
若△QRP∽△ACP,则QR:AC=RP:CP,
即:
| 3x |
| 3 |
| 4-8x |
| 4x |
∴x1=
| 2 |
| 2 |
②当P在B,R之间时,PR=8x-4,
若△PRQ∽△ACP,则PR:AC=RQ:CP,
即:
| 8x-4 |
| 3 |
| 3x |
| 4x |
∴x=
| 25 |
| 32 |
若△QRP∽△ACP,则QR:AC=RP:CP,
即:
| 3x |
| 3 |
| 8x-4 |
| 4x |
∴x1=x2=1(舍)
综上所述:存在x的值,x1=
| 2 |
| 7 |
| 32 |
| 25 |
| 32 |
点评:此题考查了相似三角形的判定和性质,根据P和R点不同位置进行分析,解题时要注意一题多解的情况,要注意别漏解是解题关键.

练习册系列答案
相关题目
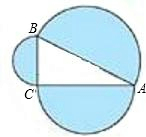 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )| A、2π | B、3π | C、4π | D、6π |
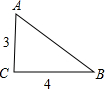
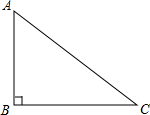 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.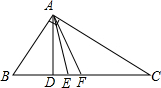 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线, 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=