题目内容
已知:如图,△ 是等边三角形,点
是等边三角形,点 、
、 分别在边
分别在边 、
、 上,
上, .
.

(1)求证:△ ∽△
∽△ ;(2)如果
;(2)如果 ,
, ,求
,求 的长.
的长.
 是等边三角形,点
是等边三角形,点 、
、 分别在边
分别在边 、
、 上,
上, .
.
(1)求证:△
 ∽△
∽△ ;(2)如果
;(2)如果 ,
, ,求
,求 的长.
的长.(1) 或
或
 或
或
试题分析:因为
 ,根据三角形相似判定定理1,易证明△
,根据三角形相似判定定理1,易证明△ ∽△
∽△ .
.(2)由△
 ∽△
∽△ ,得
,得 ,
, ,即可求
,即可求 或
或 .
.试题解析:证明:(1)∵△
 是等边三角形
是等边三角形∴
 (1分)
(1分)∵
 (1分)
(1分)又∵
 ,
,∴
 (1分)
(1分)在△
 与△
与△ 中
中
∴△
 ∽△
∽△ (2分)
(2分)(2)∵△
 ∽△
∽△
∴
 . (2分)
. (2分)设
 ,∵
,∵ 且△
且△ 是等边三角形,∴
是等边三角形,∴
∴
 ,∴
,∴ ,
, , (2分)
, (2分)∴
 或
或 . (1分)
. (1分)
练习册系列答案
相关题目
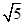 ,sinB=
,sinB=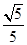 ,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.
,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.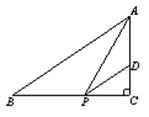
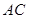 、
、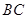 的长;
的长;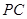 的长为
的长为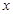 ,
,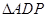 的面积为
的面积为 .当
.当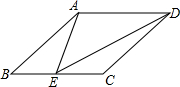


 中,点D、E分别在边AB 、AC上,下列比例式不能判定
中,点D、E分别在边AB 、AC上,下列比例式不能判定 ∥
∥ 的是( ).
的是( ).
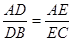 ; B.
; B.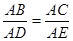 ;C.
;C. ;D.
;D. .
.
 ,BP′=
,BP′= 时,求线段AB的长.
时,求线段AB的长.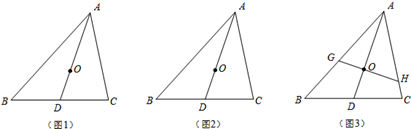
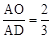 ;
;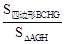 的最大值.
的最大值. ∥
∥ ∥
∥ ,
, ,
, ,
, ,则
,则 .
.