题目内容
如图,直角△ABC中,∠C=90°,AB=2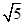 ,sinB=
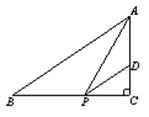
,sinB=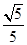 ,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.
,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.
(1)求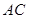 、
、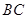 的长;
的长;
(2)设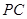 的长为
的长为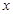 ,
,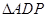 的面积为
的面积为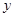 .当
.当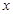 为何值时,
为何值时,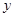 最大并求出最大值.
最大并求出最大值.
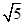 ,sinB=
,sinB=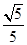 ,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.
,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.
(1)求
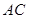 、
、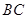 的长;
的长;(2)设
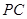 的长为
的长为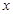 ,
,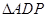 的面积为
的面积为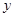 .当
.当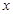 为何值时,
为何值时,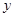 最大并求出最大值.
最大并求出最大值.(1)2,4;(2)2,1.
试题分析:(1)在Rt△ABC中,根据∠B的正弦值及斜边AB的长,可求出AC的长,进而可由勾股定理求得BC的长;
(2)由于PD∥AB,易证得△CPD∽△CBA,根据相似三角形得出的成比例线段,可求出CD的表达式,也就求出AD的表达式,进而可以AD为底、PC为高得出△ADP的面积,即可求出关于y、x的函数关系式,根据所得函数的性质,可求出y的最大值及对应的x的值.
试题解析:(1)在Rt△ABC中,
 ,
, ,
, 得
 ,
,∴AC=2,
根据勾股定理得:BC=4;
(2)∵PD∥AB,
∴△ABC∽△DPC,
∴
 ;
;设PC=x,则
 ,
, ,
,∴

∴当x=2时,y的最大值是1.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目

 的值 .
的值 . 为
为 ,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为500米.
,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为500米.
 是等边三角形,点
是等边三角形,点 、
、 分别在边
分别在边 、
、 上,
上, .
.
 ∽△
∽△ ;(2)如果
;(2)如果 ,
, ,求
,求 的长.
的长.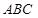 中,
中,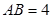 ,当直角三角板
,当直角三角板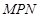 的
的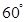 角的顶点
角的顶点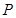 在
在 上移动时,斜边
上移动时,斜边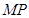 始终经过
始终经过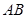 边的中点
边的中点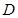 ,设直角三角板的另一直角边
,设直角三角板的另一直角边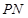 与
与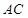 相交于点E.设
相交于点E.设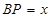 ,
,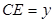 ,那么
,那么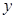 与
与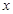 之间的函数图象大致是( )
之间的函数图象大致是( )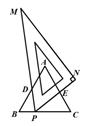
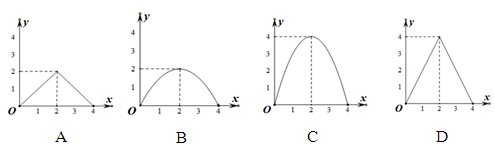


 .
.