题目内容
9.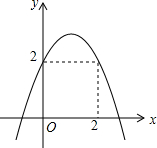 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论:①c=2;②b2-4ac<0;③当x=1时,y的最小值为a+b+c,④acb<0中,正确的有①④.
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论:①c=2;②b2-4ac<0;③当x=1时,y的最小值为a+b+c,④acb<0中,正确的有①④.
分析 根据抛物线与y轴的交点确定c的值,根据抛物线与x轴的交点情况判断b2-4ac的符号,根据对称轴确定最小值,根据开口方向确定a的符号、根据对称轴确定b的符号,判断abc的符号.
解答 解:抛物线与y轴的交点为(0,2),所以c=2,①正确;
抛物线与x轴的有两个交点,b2-4ac>0,②不正确;
对称轴不确定,所以无法确定最小值,③不正确;
开口向下,a<0,对称轴在y轴右侧,b>0,c=2>0,所以abc<0,④正确
故答案为:①④.
点评 本题考查的是二次函数的图象与系数的关系,解题的关键是理解:二次函数y=ax2+bx+c,a>0时,开口向上,a<0时,开口向下;图象与y轴的交点为(0,c),确定c的符号,根据对称轴在y轴的不同位置,确定b的符号.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
20.若A(2a-b,a+b)关于y轴对称点是A1(3,-3),则P(a,b)关于x轴对称点P1的坐标是( )
| A. | (-2,-1) | B. | (2,-1) | C. | (-2,1) | D. | (2,1) |
14.甲、乙两人从同一起点沿着同一条公路骑自行车比赛,两人同向而行,如果甲让乙先骑6m,则甲骑了6s就可追上乙;如果甲让乙先骑3s,则甲骑了4s还离乙20m;若设甲的平均速度为x m/s,乙的平均速度为y m/s,则根据题意列出方程组为( )
| A. | $\left\{\begin{array}{l}{6y=6x+6}\\{4x=7y+20}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{6x-6y=6}\\{4x=7y-20}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{6x+6=6y}\\{4x-4y=3y-20}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{6x-6=6y}\\{4x-4y=3y+20}\end{array}\right.$ |
19.下列计算正确的是( )
| A. | $(\sqrt{-3}{)^2}=-3$ | B. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | C. | $\sqrt{4}=±2$ | D. | $\sqrt{27}÷\sqrt{3}=3$ |