��Ŀ����
���������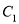 �Ķ�����������
�Ķ�����������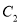 �ϣ�ͬʱ��������
�ϣ�ͬʱ��������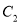 �Ķ�����������
�Ķ�����������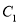 �ϣ���ô�����dz�������
�ϣ���ô�����dz�������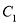 ��
��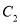 ������
������
��1����֪������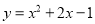 ���ж����������ߣ���
���ж����������ߣ���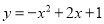 ����
����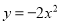
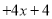 ����֪�������Ƿ��������˵�����ɣ�
����֪�������Ƿ��������˵�����ɣ�
��2����֪������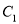 :
: 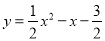 ����P������Ϊ
����P������Ϊ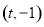 �����������Ƶ�
�����������Ƶ�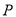 ��ת180��õ�������
��ת180��õ�������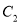 ���˴����dzƵ�PΪ��ת�㣩����������
���˴����dzƵ�PΪ��ת�㣩����������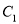 ��
��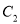 ��������������
��������������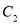 �Ľ���ʽ��
�Ľ���ʽ��
��3���ڣ�2���������£���֪��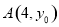 ��������
��������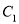 �ϵ�һ�㣬���Ե�AΪ���㲢��������
�ϵ�һ�㣬���Ե�AΪ���㲢��������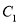 �������������
�������������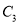 �Ľ���ʽ�����жϴ�ʱ������
�Ľ���ʽ�����жϴ�ʱ������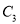 �ܷ���������
�ܷ���������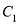 ��ת���������ܣ��������ת�����ꣻ�����ܣ���˵��������ɣ�
��ת���������ܣ��������ת�����ꣻ�����ܣ���˵��������ɣ�
��4�����������۲��룺����������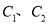 ������������ǵĶ���ʽ��ϵ�����ֱ��Ϊ
������������ǵĶ���ʽ��ϵ�����ֱ��Ϊ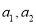 ��Ӧ����������ϵ�� ��
��Ӧ����������ϵ�� ��
�ο���ʽ���е����깫ʽ��������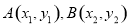 �����߶�AB���е�����Ϊ
�����߶�AB���е�����Ϊ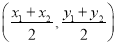 ��
��
��ϰ��ϵ�д�
�����Ŀ


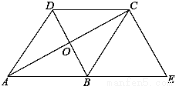
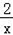 +y=1����3x��2y=1����5xy=1����
+y=1����3x��2y=1����5xy=1����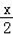 +y=1�ĸ�ʽ���У����Ƕ�Ԫһ�η��̵��У�������
+y=1�ĸ�ʽ���У����Ƕ�Ԫһ�η��̵��У�������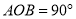 ��
�� 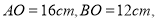 ����C�ӵ�A�������ڱ�AO����4cm/s���ٶ���O���˶������ͬʱ������D�ӵ�B�������ڱ�BO����3cm/s���ٶ���O���˶�����OC���е�E��CD�Ĵ���EF����C�˶���______sʱ����C��ΪԲ�ġ�3cmΪ�뾶��Բ��ֱ��EF���С�
����C�ӵ�A�������ڱ�AO����4cm/s���ٶ���O���˶������ͬʱ������D�ӵ�B�������ڱ�BO����3cm/s���ٶ���O���˶�����OC���е�E��CD�Ĵ���EF����C�˶���______sʱ����C��ΪԲ�ġ�3cmΪ�뾶��Բ��ֱ��EF���С�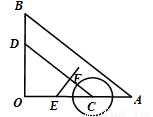
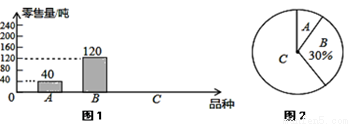
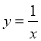 �ϣ���N��ֱ��
�ϣ���N��ֱ��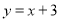 �ϣ����M����Ϊ
�ϣ����M����Ϊ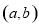 ����������
����������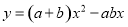 �Ķ�������Ϊ______��
�Ķ�������Ϊ______��