题目内容
 如图,△ABC的内切圆⊙O切AC于点D,∠C=90°,AD=3,BE=10,⊙O的半径是2,则BC的长为________.
如图,△ABC的内切圆⊙O切AC于点D,∠C=90°,AD=3,BE=10,⊙O的半径是2,则BC的长为________.
12
分析:利用三角形内切圆的性质,以及∠C=90°,首先得出四边形OFCD是正方形,进而得出FC=CD=DO=FO=2,再利用切线长定理即可得出答案.
解答: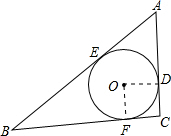 解:如图:连接DO,FO,
解:如图:连接DO,FO,
∵△ABC的内切圆⊙O切AC于点D,切BC于点F,切AB于点E,
在Rt△ABC,∠C=90°,
四边形OECF中,OD=OF,∠ODC=∠OFC=∠C=90°;
∴四边形OFCD是正方形;
∴FC=CD=DO=FO=2,
由切线长定理,得:BE=BF=10,AD=AE=3,CD=CF=2;
∴BC=BF+FC=10+2=12,
故答案为:12.
点评:此题主要考查了直角三角形内切圆性质以及切线长定理,根据已知得出四边形OFCD是正方形是解题关键.
分析:利用三角形内切圆的性质,以及∠C=90°,首先得出四边形OFCD是正方形,进而得出FC=CD=DO=FO=2,再利用切线长定理即可得出答案.
解答:
 解:如图:连接DO,FO,
解:如图:连接DO,FO,∵△ABC的内切圆⊙O切AC于点D,切BC于点F,切AB于点E,
在Rt△ABC,∠C=90°,
四边形OECF中,OD=OF,∠ODC=∠OFC=∠C=90°;
∴四边形OFCD是正方形;
∴FC=CD=DO=FO=2,
由切线长定理,得:BE=BF=10,AD=AE=3,CD=CF=2;
∴BC=BF+FC=10+2=12,
故答案为:12.
点评:此题主要考查了直角三角形内切圆性质以及切线长定理,根据已知得出四边形OFCD是正方形是解题关键.

练习册系列答案
相关题目
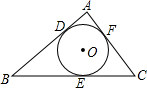 已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )
已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )| A、12 | ||
| B、14 | ||
C、10+2
| ||
D、10+
|
 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.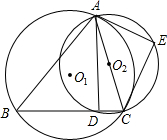 点E,连接AD、CE,若AC=7,AD=3
点E,连接AD、CE,若AC=7,AD=3
