题目内容
3. 如图,E为?ABCD的边BC延长线上一点,AE与BD交于点F,与DC交于点G.若BC=2CE,则AF:FG的值是( )
如图,E为?ABCD的边BC延长线上一点,AE与BD交于点F,与DC交于点G.若BC=2CE,则AF:FG的值是( )| A. | 3:2 | B. | 2:3 | C. | 5:3 | D. | 4:3 |
分析 根据四边形ABCD是平行四边形,得到AB∥DC,AB=DC,根据相似三角形的性质即可得到结论.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴△CEG∽△CAB,
∴$\frac{CG}{AB}=\frac{CE}{BE}$,
∵BC=2CE,
∴$\frac{CG}{AB}$=$\frac{1}{3}$,
∴$\frac{DG}{AB}$=$\frac{2}{3}$,
∵△DFG∽△BFA,
∴$\frac{AF}{FG}$=$\frac{AB}{DG}$=$\frac{3}{2}$,
故选A.
点评 此题考查了相似三角形的判定与性质以及平行四边形的性质.此题难度较大,注意掌握数形结合思想的应用,注意掌握平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似与相似三角形的对应边成比例定理的应用.

练习册系列答案
相关题目
7. 已知:如图,直线a∥b,∠1=50°.∠2=∠3,则∠2的度数为( )
已知:如图,直线a∥b,∠1=50°.∠2=∠3,则∠2的度数为( )
 已知:如图,直线a∥b,∠1=50°.∠2=∠3,则∠2的度数为( )
已知:如图,直线a∥b,∠1=50°.∠2=∠3,则∠2的度数为( )| A. | 50° | B. | 60° | C. | 65° | D. | 75° |
14.使得$\sqrt{-{a}^{2}}$有意义的a有( )
| A. | 0个 | B. | 1个 | C. | 无数个 | D. | 以上都不对 |
18.若代数式x-3的值为2,则x等于( )
| A. | 1 | B. | -1 | C. | 5 | D. | -5 |
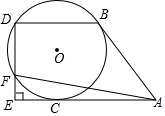 如图,AB,Ac与⊙O相切于点B,C,BD∥AC交⊙O于点D,DE⊥AC交AC的延长线于E,交⊙O于点F,∠BAF=45°.
如图,AB,Ac与⊙O相切于点B,C,BD∥AC交⊙O于点D,DE⊥AC交AC的延长线于E,交⊙O于点F,∠BAF=45°.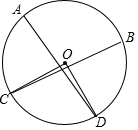 如图,已知在圆O中,劣弧AB的长度是周长的$\frac{1}{3}$,C与D在优弧AB上运动,连接AD与BC交于E点,当∠AEC=∠COD时,则∠COD=( )
如图,已知在圆O中,劣弧AB的长度是周长的$\frac{1}{3}$,C与D在优弧AB上运动,连接AD与BC交于E点,当∠AEC=∠COD时,则∠COD=( )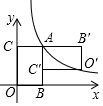 如图,矩形ABOC的顶点O在坐标原点,顶点B,C分别在x,y轴的正半轴上,顶点A在反比例函数y=$\frac{k}{x}$(k为常数,k>0,x>0)的图象上,将矩形ABOC绕点A按逆时针方向旋转90°得到矩形AB′O′C′,若点O的对应点O′恰好落在此反比例函数图象上,则$\frac{OB}{OC}$的值是$\frac{\sqrt{5}-1}{2}$.
如图,矩形ABOC的顶点O在坐标原点,顶点B,C分别在x,y轴的正半轴上,顶点A在反比例函数y=$\frac{k}{x}$(k为常数,k>0,x>0)的图象上,将矩形ABOC绕点A按逆时针方向旋转90°得到矩形AB′O′C′,若点O的对应点O′恰好落在此反比例函数图象上,则$\frac{OB}{OC}$的值是$\frac{\sqrt{5}-1}{2}$.