题目内容
10.若a是方程x2-2003x+1=0的一个根,则a2-2002a+$\frac{2003}{{a}^{2}+1}$=2002.分析 根据一元二次方程的解的定义得到a2-2003a+1=0,然后把a2=2003a-1代入代数式进行变形即可得到代数式的值.
解答 解:∵a是方程x2-2003x+1=0的一个根,
∴a2-2003a+1=0,
∴a2=2003a-1,
∴原式=2003a-1-2002a+$\frac{2003}{2003a-1+1}$
=a-1+$\frac{1}{a}$
=$\frac{{a}^{2}+1}{a}$-1
=$\frac{2003a-1+1}{a}$-1
=2003-1
=2002.
故答案为2002.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
15.下列各式:x2-y2,-x2+y2,-x2-y2,(-x)2+(-y)2,x4-y4中能用平方差公式分解因式的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
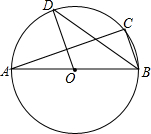 如图,AB是⊙O的直径,OB=3,BC是⊙O的弦,∠ABC的平分线交⊙O于点D,连接OD,若∠BAC=20°,则$\widehat{AD}$的长等于$\frac{7}{6}$π.
如图,AB是⊙O的直径,OB=3,BC是⊙O的弦,∠ABC的平分线交⊙O于点D,连接OD,若∠BAC=20°,则$\widehat{AD}$的长等于$\frac{7}{6}$π.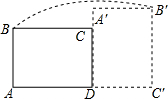 如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是$\frac{25π}{4}$+12(结果保留π).
如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是$\frac{25π}{4}$+12(结果保留π).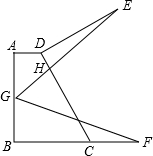 如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠DCB=60°,AD=2$\sqrt{3}$,BC=6$\sqrt{3}$,点G是线段AB中点,点F在线段BC上,连接GF,将线段GF绕点G逆时针旋转60°,得到线段GE,GE交CD于点H,连结DE,且DE⊥DC,则HE的长为$\frac{8\sqrt{21}}{3}$.
如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠DCB=60°,AD=2$\sqrt{3}$,BC=6$\sqrt{3}$,点G是线段AB中点,点F在线段BC上,连接GF,将线段GF绕点G逆时针旋转60°,得到线段GE,GE交CD于点H,连结DE,且DE⊥DC,则HE的长为$\frac{8\sqrt{21}}{3}$.