题目内容
已知,抛物线y=-
x2-2
(a-1)x-
(a2-2a)与x轴交于点A(x1,0),B(x2,0),且x1<1<x2.
(1)求A、B两点的坐标(用a表示);
(2)设抛物线的顶点为C,求△ABC的面积.
| 3 |
| 3 |
| 3 |
(1)求A、B两点的坐标(用a表示);
(2)设抛物线的顶点为C,求△ABC的面积.
考点:抛物线与x轴的交点
专题:
分析:(1)由于A、B两点是抛物线与x轴的交点,令抛物线的y=0,所得方程的根即为A、B的横坐标;
(2)根据A、B的坐标可求出AB的长,以AB为底,C点纵坐标的绝对值为高即可求出△ABC的面积.
(2)根据A、B的坐标可求出AB的长,以AB为底,C点纵坐标的绝对值为高即可求出△ABC的面积.
解答:解:(1)∵拋物线与x轴交于点A(x1,0)、B(x2,0),
∴x1、x2是关于x的方程-
x2-2
(a-1)x-
(a2-2a)=0的解;
方程可化简为x2+2(a-1)x+(a2-2a)=0;
解方程,得x=-a或x=-a+2;
∵x1<x2,-a<-a+2,(1分)
∴x1=-a,x2=-a+2
∴A、B两点的坐标分别为A(-a,0),B(-a+2,0)(2分)
(2)∵AB=2,顶点C的纵坐标为
,
∴△ABC的面积等于
.
∴x1、x2是关于x的方程-
| 3 |
| 3 |
| 3 |
方程可化简为x2+2(a-1)x+(a2-2a)=0;
解方程,得x=-a或x=-a+2;
∵x1<x2,-a<-a+2,(1分)
∴x1=-a,x2=-a+2
∴A、B两点的坐标分别为A(-a,0),B(-a+2,0)(2分)
(2)∵AB=2,顶点C的纵坐标为
| 3 |
∴△ABC的面积等于
| 3 |
点评:此题考查了二次函数与一元二次方程的关系,三角形面积的求法,熟练掌握并能灵活运用抛物线、两点间的距离公式等相关知识是解答此题的关键.

练习册系列答案
相关题目
估算
(精确到0.1)的大小是( )
| 65 |
| A、8.0 | B、8.1 |
| C、8.2 | D、8.3 |
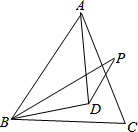 如图,D是等边△ABC内一点,DB=DA,BP=AB,∠DBP=∠DBC,求证:∠P=30°.
如图,D是等边△ABC内一点,DB=DA,BP=AB,∠DBP=∠DBC,求证:∠P=30°.