题目内容
求证：方程（x-a）（x-a-b）=1的一个根大于a，另一个小于a．
考点：抛物线与x轴的交点
专题：证明题
分析：根据函数f（x）=（x-a）（x-a-b）是开口向上的抛物线，我们易得方程（x-a）（x-a-b）=1一定有两个根，然后分b＜0，b=0，b＞0三种情况进行讨论，易得到结论．
解答：证明：（x-a）（x-a-b）=0的两个根为a，a+b，
则方程（x-a）（x-a-b）=1一定有两个根，
设方程（x-a）（x-a-b）=1的两根为m，n，
当b＜0时，m＜a+b＜a＜n，
当b=0时，m＜a＜n，
当b＞0时，m＜a＜a+b＜n，
则方程（x-a）（x-a-b）=1（a、b∈R）的根一定一根大于a，一根小于a．
则方程（x-a）（x-a-b）=1一定有两个根，
设方程（x-a）（x-a-b）=1的两根为m，n，
当b＜0时，m＜a+b＜a＜n，
当b=0时，m＜a＜n，
当b＞0时，m＜a＜a+b＜n，
则方程（x-a）（x-a-b）=1（a、b∈R）的根一定一根大于a，一根小于a．
点评：本题考查的知识点是抛物线与x轴的交点，一元二次方程的根的分布情况，根据函数零点与对应方程根的关系，利用函数图象分析函数根的分布情况是解答本题的关键．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
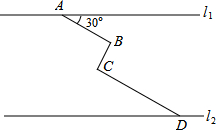如图，在同一平面内，两条平行高速公路l1和l2间有一条“Z”型道路连通，其中AB段与高速公路l1成30°角，长为20km； BC段与AB、CD段都垂直，BC段长为10km，CD段长为30km．则两条高速公路l1和l2间的距离为