题目内容
在一次家庭年收入的调查中,抽查了15个家庭的年收入如下表所示(单位:万元):| 家庭个数 | 每个家庭的年收入 |
| 1 | 0.9 |
| 3 | 1.0 |
| 3 | 1.2 |
| 1 | 1.3 |
| 3 | 1.4 |
| 3 | 1.6 |
| 1 | 18.2 |
(1)样本的平均数= 万元;
(2)样本的中位数= 万元;
(3)样本的标准差= 万元(结果保留到小数点后第一位).
(4)你认为在平均数和中位数中,哪一个更能描述这个样本的集中趋势? 为什么? .
【答案】分析:(1)要求平均数只要求出数据之和再除以总个数即可;
(2)对于中位数,因图中是按从小到大的顺序排列的,所以只要找出最中间的一个数即可;
(3)先算方差,再算标准差;
(4)中位数更能描述集中趋势,因为平均数受到极端值18.2的影响大.
解答:解:(1)根据平均数的定义:样本的平均数=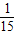 (0.9×1+1.0×3+1.2×3+1.3×1+1.4×3+1.6×3+18.2×1)=2.4(万元);
(0.9×1+1.0×3+1.2×3+1.3×1+1.4×3+1.6×3+18.2×1)=2.4(万元);
(2)排序后第8个数为1.3万元,故样本的中位数为1.3(万元).
(3)先算方差,再算标准差;S2=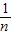 [(x1-
[(x1-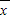 )2+(x2-
)2+(x2-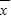 )2+…+(xn-
)2+…+(xn-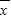 )2]=17.64,
)2]=17.64,
所以标准差S=4.2万元.
(4)更能描述这个样本的集中趋势是中位数.因为平均数受到极端值18.2的影响大,所以此题要选择中位数描述集中趋势.
故填2.4;1.3;4.2;中位数,平均数受到极端值18.2的影响大.
点评:本题考查统计知识中的平均数、中位数、方差和标准差.将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.
方差公式为:S2=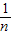 [(x1-
[(x1-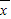 )2+(x2-
)2+(x2-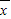 )2+…+(xn-
)2+…+(xn-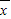 )2].标准差是方差的算术平方根.
)2].标准差是方差的算术平方根.
(2)对于中位数,因图中是按从小到大的顺序排列的,所以只要找出最中间的一个数即可;
(3)先算方差,再算标准差;
(4)中位数更能描述集中趋势,因为平均数受到极端值18.2的影响大.
解答:解:(1)根据平均数的定义:样本的平均数=
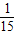 (0.9×1+1.0×3+1.2×3+1.3×1+1.4×3+1.6×3+18.2×1)=2.4(万元);
(0.9×1+1.0×3+1.2×3+1.3×1+1.4×3+1.6×3+18.2×1)=2.4(万元);(2)排序后第8个数为1.3万元,故样本的中位数为1.3(万元).
(3)先算方差,再算标准差;S2=
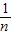 [(x1-
[(x1-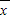 )2+(x2-
)2+(x2-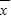 )2+…+(xn-
)2+…+(xn-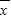 )2]=17.64,
)2]=17.64,所以标准差S=4.2万元.
(4)更能描述这个样本的集中趋势是中位数.因为平均数受到极端值18.2的影响大,所以此题要选择中位数描述集中趋势.
故填2.4;1.3;4.2;中位数,平均数受到极端值18.2的影响大.
点评:本题考查统计知识中的平均数、中位数、方差和标准差.将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.
方差公式为:S2=
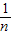 [(x1-
[(x1-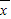 )2+(x2-
)2+(x2-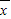 )2+…+(xn-
)2+…+(xn-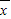 )2].标准差是方差的算术平方根.
)2].标准差是方差的算术平方根. 
练习册系列答案
相关题目
在一次家庭年收入的调查中,抽查了15个家庭的年收入如下表所示(单位:万元):
根据表中提供的信息,填空:
(1)样本的平均数= 万元;
(2)样本的中位数= 万元;
(3)样本的标准差= 万元(结果保留到小数点后第一位).
(4)你认为在平均数和中位数中,哪一个更能描述这个样本的集中趋势? 为什么? .
| 家庭个数 | 每个家庭的年收入 |
| 1 | 0.9 |
| 3 | 1.0 |
| 3 | 1.2 |
| 1 | 1.3 |
| 3 | 1.4 |
| 3 | 1.6 |
| 1 | 18.2 |
(1)样本的平均数=
(2)样本的中位数=
(3)样本的标准差=
(4)你认为在平均数和中位数中,哪一个更能描述这个样本的集中趋势?
在一次家庭年收入的调查中,抽查了15个家庭的年收入(单位:万元)如下表所示:
|
家庭个数 |
每个家庭的年收入 |
|
1 |
0.9 |
|
3 |
1.0 |
|
3 |
1.2 |
|
1 |
1.2 |
|
3 |
1.4 |
|
3 |
1.6 |
|
1 |
18.2 |
根据表中提供的信息,填空:
(1)样本的平均数x=________万元;
(2)样本的中位数=________万元;
(3)样本的标准差σ=________万元(结果保留到小数点后第一位).
(4)你认为在平均数和中位数中,哪一个更能描述这个样本的集中趋势?为什么?
在一次家庭年收入的调查中,抽查了15个家庭的年收入如下表所示(单位:万元):
| 家庭个数 | 每个家庭的年收入 |
| 1 | 0.9 |
| 3 | 1.0 |
| 3 | 1.2 |
| 1 | 1.3 |
| 3 | 1.4 |
| 3 | 1.6 |
| 1 | 18.2 |
(1)样本的平均数=______万元;
(2)样本的中位数=______万元;
(3)样本的标准差=______万元(结果保留到小数点后第一位).
(4)你认为在平均数和中位数中,哪一个更能描述这个样本的集中趋势?______为什么?______.
在一次家庭年收入的调查中,抽查了15个家庭的年收入如下表所示(单位:万元):
根据表中提供的信息,填空:
(1)样本的平均数= 万元;
(2)样本的中位数= 万元;
(3)样本的标准差= 万元(结果保留到小数点后第一位).
(4)你认为在平均数和中位数中,哪一个更能描述这个样本的集中趋势? 为什么? .
| 家庭个数 | 每个家庭的年收入 |
| 1 | 0.9 |
| 3 | 1.0 |
| 3 | 1.2 |
| 1 | 1.3 |
| 3 | 1.4 |
| 3 | 1.6 |
| 1 | 18.2 |
(1)样本的平均数= 万元;
(2)样本的中位数= 万元;
(3)样本的标准差= 万元(结果保留到小数点后第一位).
(4)你认为在平均数和中位数中,哪一个更能描述这个样本的集中趋势? 为什么? .