Question

10．如图，⊙O的直径AB的长为10，弦AC的长为5，∠ACB的平分线交⊙O于点D．
（1）求BC的长；（2）求弦BD的长．

Answer 1

分析 （1）由圆周角定理可知△ABC为直角三角形，利用勾股定理可求得BC；
（2）由条件可知D为$\widehat{AB}$的中点，则可知AD=BD，利用勾股定理可求得BD的长．

解答 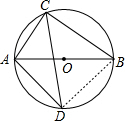解：
（1）∵AB为直径，
∴∠ACB=90°，
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{1{0}^{2}-{5}^{2}}$=5$\sqrt{3}$；
（2）如图，连接BD，同理可知∠ADB=90°，
∵CD平分∠ACB，
∴∠ACD=∠BCD，
∴AD=BD，
∵AD²+BD²=AB²，
∴2BD²=100，解得BD=5$\sqrt{2}$．

点评 本题主要考查圆周角定理，掌握直径所对的圆周角为直角是解题的关键．