题目内容
菱形ABCD的边长为5cm,其中一条对角线长为6cm,则另一条对角线的长为
8
8
cm,菱形的面积为24
24
cm2.分析:根据菱形性质得出AC=2AO=2OC=6cm,BD=2BO,AC⊥BD,求出OA=3cm,∠AOB=90°,由勾股定理求出OB,得出BD=2OB=8cm,代入
AC×BD求出即可.
| 1 |
| 2 |
解答:解: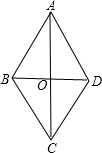
∵四边形ABCD是菱形,
∴AC=2AO=2OC=6cm,BD=2BO,AC⊥BD,
∴OA=3cm,∠AOB=90°,
由勾股定理得:OB=
=
=4(cm),
∴BD=2OB=8cm,
菱形ABCD的面积是
AC×BD=
×6cm×8cm=24cm2,
故答案为:8、24.

∵四边形ABCD是菱形,
∴AC=2AO=2OC=6cm,BD=2BO,AC⊥BD,
∴OA=3cm,∠AOB=90°,
由勾股定理得:OB=
| AB2-AO |
| 52-32 |
∴BD=2OB=8cm,
菱形ABCD的面积是
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:8、24.
点评:本题考查了菱形性质和勾股定理,注意:菱形的对角线互相垂直平分,菱形ABCD的面积=
AC×BD.
| 1 |
| 2 |

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 已知:如图,菱形ABCD的边长为4,∠A=60°,以点A为圆心,AD长为半径画弧,以点B为圆心,BC长为半径画弧,则图中阴影部分的面积是
已知:如图,菱形ABCD的边长为4,∠A=60°,以点A为圆心,AD长为半径画弧,以点B为圆心,BC长为半径画弧,则图中阴影部分的面积是 如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2. 25、菱形ABCD的边长为24厘米,∠A=60°,质点P从点A出发沿着AB-BD-DA作匀速运动,质点Q从点D同时出发沿着线路DC-CB-BD作匀速运动.
25、菱形ABCD的边长为24厘米,∠A=60°,质点P从点A出发沿着AB-BD-DA作匀速运动,质点Q从点D同时出发沿着线路DC-CB-BD作匀速运动. 面积.
面积.