题目内容
1．用适当方法解下列方程：（1）x2-7x+6=0
（2）3x（x+2）=4（x+2）
分析 （1）方程利用因式分解法求出解即可；
（2）方程移项后，利用因式分解法求出解即可．
解答 解：（1）分解因式得：（x-1）（x-6）=0，
可得x-1=0或x-6=0，
解得：x1=1，x2=6；
（2）方程移项得：3x（x+2）-4（x+2）=0，
分解因式得：（3x-4）（x+2）=0，
解得：x1=$\frac{4}{3}$，x2=-2．
点评 此题考查了解一元二次方程-因式分解法，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
11．一检查小组从某品牌奶粉中抽取样品16袋，检测每袋的质量是否符合标准，若标准质量为250克，将超过的克数记为正数，不足的克数记为负数，偏差结果记录如下：
（1）与标准比较，这16袋奶粉的总计超过多少克或不足多少克？
（2）这16袋食品的总质量是多少？
| 与标准质量的差值（单位：g） | -8 | -3 | 0 | 2 | 4 |
| 序号 | 4 | 3 | 6 | 2 | 1 |
（2）这16袋食品的总质量是多少？
如图，C为线段AB上一点，AB-BC=10cm，BC：AC=3：5．求AB的长．
如图，有一个长、宽、高分别为50cm、40cm、30cm的木箱，你能否把一根长为70cm的木棒放进去？请说明你的理由．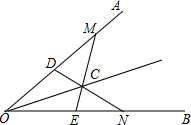
如图，小明用三角尺画∠AOB的平分线，他先在∠AOB两边OA，OB上分别取OM=ON，OD=OE，然后，连接DN和EM，相交于点C，再作射线OC，此时他认为OC就是∠AOB的平分线，你认为他的做法正确吗？请说明理由．
如图是几个小正方体所搭的几何体的俯视图，小正方形中数字表示该位置的小正方体的个数，请画出该几何体的主视图和左视图．
14．60的$\frac{2}{5}$相当于80的（ ）
| A． | $\frac{3}{8}$ | B． | $\frac{3}{10}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{4}$ |