题目内容
11.如图a,有两个全等的正三角形ABC和DEF,点D、C分别为△ABC、DEF的内心;固定点D,将△DEF顺时针旋转,使得DF经过点C,如图b,则图a中四边形CNDM与图b中△CDM面积的比为( )
| A. | 2:1 | B. | 2:$\sqrt{3}$ | C. | 4:3 | D. | $\sqrt{3}$:$\sqrt{2}$ |
分析 连接MN、CD.由等三角形的性质可知∠DCM=30°,设MN的长为a,CD=$\sqrt{3}$a,由四边形CNDM的面积=$\frac{1}{2}$MN•CD可求得四边形CNDM的面积,然后在△DCM中,依据特殊锐角三角函数值可求得DM、CM的长,依据三角形的面积公式可求得△CDM的面积,从而可求得答案.
解答 解:如图所示:连接MN、CD.
设MN的长为a,CD=$\sqrt{3}$a,则四边形CNDM的面积=$\frac{1}{2}$MN•CD=$\frac{1}{2}$×a×$\sqrt{3}$a=$\frac{\sqrt{3}}{2}$a2,
∵∠DCM=30°,∠CDM=60°,
∴DM=$\frac{1}{2}$DC=$\frac{\sqrt{3}}{2}a$,CM=$\frac{3}{2}$a.
∴△CDM=$\frac{1}{2}$DM•CM=$\frac{1}{2}$×$\frac{\sqrt{3}a}{2}$×$\frac{3a}{2}$=$\frac{3\sqrt{3}}{8}$a2.
∴四边形CNDM与图b中△CDM面积的比=4:3.
故选;C.
点评 本题主要考查的是三角形的内心、旋转的性质、等边三角形的性质、特殊锐角三角函数的应用,依据特殊锐角三角函数值求得MN、DC、DM、CM之间的关系是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
20. 如图,面积为24的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=$\frac{\sqrt{6}}{2}$,则小正方形的周长为( )
如图,面积为24的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=$\frac{\sqrt{6}}{2}$,则小正方形的周长为( )
 如图,面积为24的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=$\frac{\sqrt{6}}{2}$,则小正方形的周长为( )
如图,面积为24的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=$\frac{\sqrt{6}}{2}$,则小正方形的周长为( )| A. | $\frac{5\sqrt{6}}{8}$ | B. | $\frac{5\sqrt{6}}{6}$ | C. | $\frac{5\sqrt{6}}{2}$ | D. | $\frac{10\sqrt{6}}{3}$ |
1.下列说法正确的是( )
| A. | 了解我国青年人喜欢的电视节目应作全面调查 | |
| B. | “购买1张彩票就中奖”是不可能事件 | |
| C. | “任意画出一个平行四边形,它是中心对称图形”是必然事件 | |
| D. | 甲、乙两组数据,若${{S}_{甲}}^{2}$>${{S}_{乙}}^{2}$,则乙组数据离散程度大 |
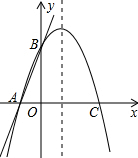 如图,已知直线y=3x+3与x轴交于点A,与y轴交于点B,过A,B两点的抛物线交x轴于另一点C(3,0).
如图,已知直线y=3x+3与x轴交于点A,与y轴交于点B,过A,B两点的抛物线交x轴于另一点C(3,0).
 如图,甲、乙是两个不透明的圆桶,甲桶内的三张牌分别标记数字2,3,4乙桶内的两张分别标记数字1,2(这些牌除所标数字不同外,其余均相同).若小宇从甲乙两个圆桶中各随机抽出一张牌,其数字之和大于4的概率是$\frac{1}{2}$.
如图,甲、乙是两个不透明的圆桶,甲桶内的三张牌分别标记数字2,3,4乙桶内的两张分别标记数字1,2(这些牌除所标数字不同外,其余均相同).若小宇从甲乙两个圆桶中各随机抽出一张牌,其数字之和大于4的概率是$\frac{1}{2}$. 在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心,OB长为半径的圆交BC于D,DE⊥AC交AC于E.
在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心,OB长为半径的圆交BC于D,DE⊥AC交AC于E.