题目内容
请看有理化分母:
(一)
=
=
;
(二)
=
=
;
(三)
=
=
=
-1;
(四)
=
=
=
=
-1;
(1)请用不同的方法化简
.
(2)化简
+
+
+…+
.
(一)
| 3 | ||
|
3×
| ||||
|
| 3 |
| 5 |
| 5 |
(二)
|
|
| ||
| 3 |
(三)
| 2 | ||
|
2(
| ||||
(
|
2(
| ||
(
|
| 3 |
(四)
| 2 | ||
|
| 3-1 | ||
|
(
| ||
|
(
| ||||
|
| 3 |
(1)请用不同的方法化简
| 2 | ||||
|
(2)化简
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
分析:(1)此题有两种不同的做法,第一个方法是把分子与分母同时乘以分母的有理化因式(
-
),再进行计算即可;第二个计算方法是把分子进行整理,再利用平方差公式进行分解,即可求出结果.
(2)先把分子与分母进行有理化,再进行统分,然后把分子中的各项进行抵消,即可求出答案.
| 5 |
| 3 |
(2)先把分子与分母进行有理化,再进行统分,然后把分子中的各项进行抵消,即可求出答案.
解答:解:(1)方法一:
=
=
=
-
;
方法二:
=
=
=
-
;
(2)
+
+
+…+
=
+
+
+…+
,
=
=
=
.
| 2 | ||||
|
2(
| ||||||||
(
|
2(
| ||||
| 2 |
| 5 |
| 3 |
方法二:
| 2 | ||||
|
(
| ||||
|
(
| ||||||||
|
| 5 |
| 3 |
(2)
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
=
| ||
| 2 |
| ||||
| 2 |
| ||||
| 2 |
| ||||
| 2 |
=
(
| ||||||||||||||
| 2 |
=
| ||||||||||||||
| 2 |
=
| ||
| 2 |
点评:此题考查了分母有理化,利用平方差公式找出分子与分母中的有理化因式,再进行分母有理化是解题的关键.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
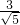 =
= ;
;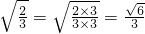 ;
;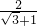 =
= =
= ;
;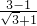 =
=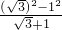 =
=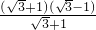 =
= ;
;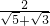 .
. .
. =
= ;
; ;
; =
= =
= ;
; =
= =
= =
= =
= ;
; .
. .
.