题目内容
如图（10），EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD。
解：∵EF∥AD，
∴∠2= （ ）
又∵∠1=∠2，
∴∠1=∠3，
∴AB∥ （ ）
∴∠BAC+ =180°（ ）
∵∠BAC=70 °，∴∠AGD= 。
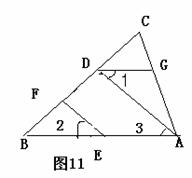
如图（10），EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD。
解：∵EF∥AD，
∴∠2= ∠ 3 （两直线平行，同位角相等）
又∵∠1=∠2，
∴∠1=∠3，
∴AB∥ DG （内错角相等，两直线平行）
∴∠BAC+ ∠AGD =180°（两直线平行，同旁内角互补）
∵∠BAC=70 °，∴∠AGD= 110 ° 。
练习册系列答案
相关题目
为
边BC上的一点，AE⊥DE，AB=12，BE=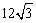
，F为线段BE上一点，EF=7，连接AF。如图1，现有一张硬纸片△GMN，∠NGM=900，NG=6，MG=
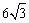，斜边MN与边BC在同一直线上，点N与点E重合，点G在线段DE上。如图2，△GMN从图1的位置出发，以每秒1个单位的速度沿EB向点B匀速移动，同时，点P从A点
出发，以每秒2个单位的速度沿AD向点D匀速移动，点Q为直线GN与线段AE的交点，连接PQ。当点G到达线段AE上时，△GMN和点P同时停止运动。设运动时间为t秒，解答问题：
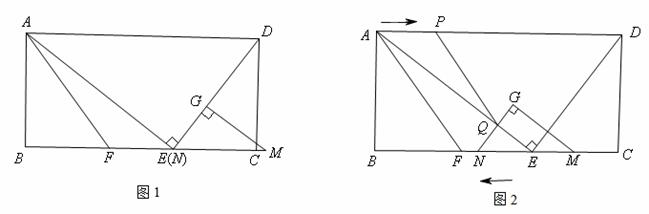
°，求∠EAD、∠DAC、∠C的度数。（6分）
