Question

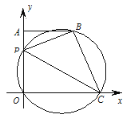
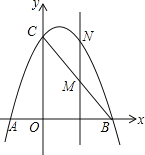
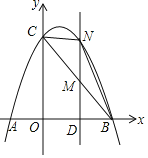
【题目】如图，已知抛物线y＝ax2+bx+3经过点A（﹣1，0）、B（3，0）两点，且交y轴交于点C．

（1）求抛物线的解析式；

（2）点M是线段BC上的点（不与B、C重合），过M作MN∥y轴交抛物线于N，若点M的横坐标为m，请用m的代数式表示MN的长；

（3）在（2）的条件下，连接NB，NC，是否存在点M，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由．

Answer 1

【答案】（1）y＝﹣x2+2x+3；（2）MN＝﹣m2+3m（0＜m＜3）；（3）存在，当m＝时，△BNC的面积最大，最大值为

【解析】

（1）直接利用待定系数法即可求出抛物线的解析式；

（2）先利用待定系数法求出直线BC的解析式，已知点M的横坐标，代入直线BC、抛物线的解析式中，可得到M、N点的坐标，N、M纵坐标的差的绝对值即为MN的长；

（3）根据题（1）（2）的结论，列出关于m的表达式，再利用函数的性质求解的最大值即可.

（1）抛物线经过点两点，代入得：

，解得：

则抛物线的解析式为；

（2）由抛物线可知，

因此，设直线BC的解析式为：

代入得

解得：

则直线BC的解析式：

已知点M的横坐标为m，且轴，则；

则

故MN的长为；

（3）存在点M，使的面积最大

如图，过点M作轴于点D

则

即

由二次函数的性质可知：当时，随m的增大而增大；当时，随m的增大而减小

则当时，的面积最大，最大值为.