题目内容
14.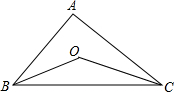 如图,∠ABC与∠ACB的角平分线BO,CO相交于点O,∠A=100°,则∠B0C=( )
如图,∠ABC与∠ACB的角平分线BO,CO相交于点O,∠A=100°,则∠B0C=( )| A. | 60° | B. | 100° | C. | 130° | D. | 140° |
分析 先求出∠ABC+∠ACB的度数,根据平分线的定义得出∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,求出∠OBC+∠OCB的度数,根据三角形内角和定理求出即可.
解答 解:∵∠A=100°,
∴∠ABC+∠ACB=180°-∠A=80°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=40°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-40°=140°.
故选D.
点评 本题考查了三角形内角和定理,角平分线定义的应用,注意:三角形的内角和等于180°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知点A、B在数轴上分别表示数a、b.
(1)观察数轴并填写下表:(最后一列由你自己选取两个数)
(2)若设A、B两点间的距离为c,则c可表示为D
A.a+b B.a-b C.|a+b|D.|a-b|
(3)求|x-2|=1中x的值.
(1)观察数轴并填写下表:(最后一列由你自己选取两个数)
| a | 5 | 4 | -2 | -3 | 2 | |
| b | 3 | 0 | -1 | 0 | -4 | |
| A、B两点间的距离 | 2 | 3 | 3 |
A.a+b B.a-b C.|a+b|D.|a-b|
(3)求|x-2|=1中x的值.
2.若a<$\sqrt{20}$<b,其中a,b是两个连续的整数,则a+b=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
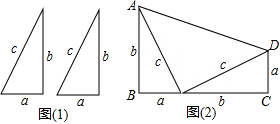
 如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别是点D,E,则PE=PD(图中相等的线段,只写一对)
如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别是点D,E,则PE=PD(图中相等的线段,只写一对)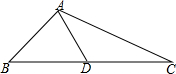 如图,△ABC中,AB=1,AC=$\sqrt{3}$,边BC上的中线AD=$\frac{\sqrt{2}}{2}$,则BC=$\sqrt{6}$.
如图,△ABC中,AB=1,AC=$\sqrt{3}$,边BC上的中线AD=$\frac{\sqrt{2}}{2}$,则BC=$\sqrt{6}$.