题目内容
11. 如图,△ABC中,D为BC边上一点,AD的垂直平分线交AD于E,交BC的延长线于点F,且∠CAF=∠B,说明:AD平分∠BAC.
如图,△ABC中,D为BC边上一点,AD的垂直平分线交AD于E,交BC的延长线于点F,且∠CAF=∠B,说明:AD平分∠BAC.
分析 由EF是AD的垂直平分线,可得AF=DF,然后由等边对等角,可证得∠EAF=∠EDF,然后利用三角形外角的性质与∠FAC=∠B,可证得AD平分∠BAC.
解答 证明:∵EF是AD的垂直平分线,
∵AF=DF,
∴∠EAF=∠EDF,
∵∠EAF=∠FAC+∠CAD,∠EDF=∠BAD+∠B,
又∵∠FAC=∠B,
∴∠BAD=∠CAD,
即AD平分∠BAC.
点评 此题主要考查了线段垂直平分线的性质,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2.若(2x-5y)2=4x2+mxy+25y2,则m的值为( )
| A. | 20 | B. | -20 | C. | -10 | D. | ±20 |
16.下列说法中错误的是( )
| A. | 0和x都是单项式 | B. | -$\frac{2x+y}{2}$与$\frac{1}{x}$都不是单项式 | ||
| C. | a2-3ab+2b3 是三次三项式 | D. | -2πx2y的系数是-2,次数是3 |
1.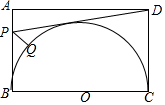 如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )
如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )
 如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )
如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )| A. | 5 | B. | $\sqrt{13}$+2 | C. | $\frac{\sqrt{73}}{2}$+$\frac{1}{2}$ | D. | 3$\sqrt{5}$-2 |