题目内容
1.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)求证:EG=CG;EG⊥CG.
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
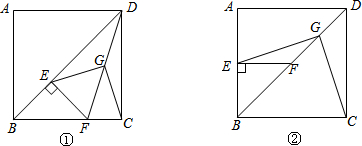
分析 (1)根据直角三角形斜边中线的性质以及三角形外角定理即可证明.
(2)作GM⊥BC于M,⊥AB于N交CD于H,只要证明△GNE≌△GMC即可解决问题.
解答 证明:(1)如图①中,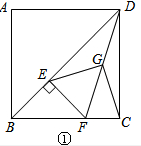 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴∠BCD=∠ADC=90°,∠BDC=$\frac{1}{2}∠ADC=45°$,
∵EF⊥BD,
∴∠DEF=90°,
∵GF=GD,
∴EG=DG=GF=$\frac{1}{2}$DF,GC=DG=GF=$\frac{1}{2}$DF,
∴EG=GC,∠GED=∠GDE,∠GCD=∠GDC,
∵∠EGF=∠GED+∠GDE=2∠EDG,∠CGF=∠GCD+∠GDC=2∠GDC,
∴∠EGC=∠EGF+∠CGF=2∠EDG+2∠GDC=2(∠EDG+∠GDC)=90°,
∴EG⊥GC.
(2)图②中,结论仍然成立.
理由: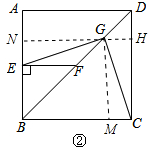 作GM⊥BC于M,⊥AB于N交CD于H.
作GM⊥BC于M,⊥AB于N交CD于H.
∵四边形ABCD是正方形,
∴∠A=∠ADC=90°,∠ABD=∠DBC=∠BDC=45°
∴GM=GN,
∵∠A=∠ANG=∠ADH=90°,
∴四边形ANHD是矩形,
∴∠DHN=90°,∠GDH=∠HGD=45°,
∴HG=DH=AN,同理GH=CM,
∵∠ENG=∠A=∠BEF=90°,
∴EF∥GN∥AD,∵GF=GD,
∴AN=NE=GH=MC,
在△GNE和△GMC中,
$\left\{\begin{array}{l}{GN=GM}\\{∠GNE=∠GMC=90°}\\{NE=MC}\end{array}\right.$,
∴△GNE≌△GMC,
∴GE=GC,∠NGE=∠MGC,
∴∠EGC=∠NGM=90°,
∴EG⊥GC.
点评 本题考查全等三角形的判定和性质、正方形的性质、矩形的判定和性质等知识,添加辅助线构造全等三角形是解决问题的关键,属于中考常考题型.

| A. | $3\sqrt{3}$ | B. | 6 | C. | 3 | D. | $2\sqrt{6}$ |
| A. | x2-2x+1 | B. | 1+4x2 | C. | a2+ab+b2 | D. | x2+2x-1 |
 快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题:
快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题: