题目内容
如图,⊙O中,直径MN=10 ,正方形ABCD四个顶点分别在半径OM、OP以及⊙O上,并且∠POM = 45°,则 AB长为 .

【答案】
 .
.
【解析】
试题分析:∵∠POM=45°,∠DCO=90°,∴∠DOC=∠CDO=45°,∴△CDO为等腰直角三角形,那么CO=CD.连接OA,可得到直角三角形OAB,∴AB=BC=CD=CO,BO=BC+CO=BC+CD=2AB,那么AB2+OB2=52,∴AB2+(2AB)2=52,∴AB的长为 .
.

考点:正多边形和圆.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
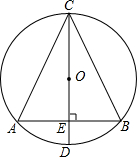 如图,⊙O中,直径CD垂直于弦AB于E,AB=2,连接AC,BC,则tan∠ACB的值的倒数等于线段( )
如图,⊙O中,直径CD垂直于弦AB于E,AB=2,连接AC,BC,则tan∠ACB的值的倒数等于线段( )| A、AC的长 | B、AE的长 | C、OE的长 | D、CE的长 |
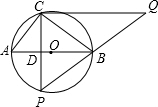 已知:如图,⊙O中,直径AB=5,在它的不同侧有定点C和动点P,BC:CA=4:3,点P在
已知:如图,⊙O中,直径AB=5,在它的不同侧有定点C和动点P,BC:CA=4:3,点P在
 20、如图,⊙O中,直径CD⊥弦AB于E点,若CD=10,DE=2,求AB的长.
20、如图,⊙O中,直径CD⊥弦AB于E点,若CD=10,DE=2,求AB的长. 如图:⊙O中,直径AB⊥直径CD,点E在OA上,EF⊥CE交BD于点F,EF交CD于M.CF交AB于N.
如图:⊙O中,直径AB⊥直径CD,点E在OA上,EF⊥CE交BD于点F,EF交CD于M.CF交AB于N. 如图在⊙O中,直径AB⊥弦CD,垂足为P,∠BAD=30°,则∠AOC的度数是
如图在⊙O中,直径AB⊥弦CD,垂足为P,∠BAD=30°,则∠AOC的度数是