题目内容
 如图:⊙O中,直径AB⊥直径CD,点E在OA上,EF⊥CE交BD于点F,EF交CD于M.CF交AB于N.
如图:⊙O中,直径AB⊥直径CD,点E在OA上,EF⊥CE交BD于点F,EF交CD于M.CF交AB于N.(1)求证:EC=EF;
(2)若AE=1,DM=
| 5 | 3 |
分析:(1)连接AD、AC、ED,利用垂直平分线的性质以及等角对等边得出ED=EF,进而得出答案即可;
(2)设OM=x,则OC=x+
,OE=x+
,由△EOM∽△COE,得OE2=OM•OC,解出x=
,所以OC=3,OE=2,EC=
,进而证明△ENC∽△ECB,得EC2=EN•EB,可求EN=
,则可求出△ENC的面积.
(2)设OM=x,则OC=x+
| 5 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 13 |
| 13 |
| 5 |
解答:(1)证明:连接AD、AC、ED.
∵直径AB⊥直径CD,
∴AD=AC;
∵AB⊥CD,EF⊥CE,
∴∠BEF=∠ECD=∠EDC,于是∠EDB=∠EDC+45°=∠BEF+45°=∠EFD,
所以ED=EF,即EC=EF;
(2)解:设OM=x,则OC=x+
,OE=x+
,
∵∠CEO+∠OEM=90°,∠OEM+∠EMO=90°,
∴∠COE=∠EMO,
又∵∠COE=∠EOM=90°,
∴△EOM∽△COE,
得OE2=OM•OC,
(x+
) 2=x•(x+
),
解得:x=
,
所以OC=3,OE=2,EC=
,
∵直径AB⊥直径CD,
∴AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵CE⊥EF,
EC=EF,
∴∠ECF=∠EFC=45°,
∴∠CBE=∠ECF=45°,
又∵∠CEN=∠BEC,
∴△ENC∽△ECB,
∴EC2=EN•EB,
(
)2=EN•5,
解得EN=
.
则S△ENC=
EN•OC=3.9.
∵直径AB⊥直径CD,
∴AD=AC;
∵AB⊥CD,EF⊥CE,
∴∠BEF=∠ECD=∠EDC,于是∠EDB=∠EDC+45°=∠BEF+45°=∠EFD,
所以ED=EF,即EC=EF;
(2)解:设OM=x,则OC=x+
| 5 |
| 3 |
| 2 |
| 3 |
∵∠CEO+∠OEM=90°,∠OEM+∠EMO=90°,
∴∠COE=∠EMO,
又∵∠COE=∠EOM=90°,

∴△EOM∽△COE,
得OE2=OM•OC,
(x+
| 2 |
| 3 |
| 5 |
| 3 |
解得:x=
| 4 |
| 3 |
所以OC=3,OE=2,EC=
| 13 |
∵直径AB⊥直径CD,
∴AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵CE⊥EF,
EC=EF,
∴∠ECF=∠EFC=45°,
∴∠CBE=∠ECF=45°,
又∵∠CEN=∠BEC,
∴△ENC∽△ECB,
∴EC2=EN•EB,
(
| 13 |
解得EN=
| 13 |
| 5 |
则S△ENC=
| 1 |
| 2 |
点评:此题主要考查了圆的综合应用以及相似三角形的判定与性质,根据已知得出△ENC∽△ECB是解题关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
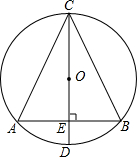 如图,⊙O中,直径CD垂直于弦AB于E,AB=2,连接AC,BC,则tan∠ACB的值的倒数等于线段( )
如图,⊙O中,直径CD垂直于弦AB于E,AB=2,连接AC,BC,则tan∠ACB的值的倒数等于线段( )| A、AC的长 | B、AE的长 | C、OE的长 | D、CE的长 |
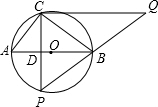 已知:如图,⊙O中,直径AB=5,在它的不同侧有定点C和动点P,BC:CA=4:3,点P在
已知:如图,⊙O中,直径AB=5,在它的不同侧有定点C和动点P,BC:CA=4:3,点P在
 20、如图,⊙O中,直径CD⊥弦AB于E点,若CD=10,DE=2,求AB的长.
20、如图,⊙O中,直径CD⊥弦AB于E点,若CD=10,DE=2,求AB的长. 如图在⊙O中,直径AB⊥弦CD,垂足为P,∠BAD=30°,则∠AOC的度数是
如图在⊙O中,直径AB⊥弦CD,垂足为P,∠BAD=30°,则∠AOC的度数是