题目内容
【题目】背景情境:
赛赛同学在学习《一元二次方程》中做过这样一道题:
题目:已知实数![]() 、
、![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:根据题意得
![]() 与
与![]() 为方程
为方程![]() 的两根,
的两根,
∴![]() ,
,![]()
∴![]()
请认真阅读赛赛同学解题的方法,仔细思考.
解决问题:
(1)已知实数![]() 、
、![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(2)设实数![]() 、
、![]() 分别满足
分别满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(3)已知关于![]() 的方程
的方程![]() 有两个根
有两个根![]() 、
、![]() 满足
满足![]() .当
.当![]() 的三边
的三边![]() 、
、![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() (a≠b).求
(a≠b).求![]() 的值以及
的值以及![]() 的面积.
的面积.
【答案】(1)-6;(2)6;(3)![]() ,面积为1
,面积为1
【解析】
(1)根据题意可得![]() ,
,![]() ,利用完全平方公式求得
,利用完全平方公式求得![]() 的值,变形整理所求式子,然后代入求值即可;
的值,变形整理所求式子,然后代入求值即可;
(2)将方程![]() 等号两边同时除以b2得到
等号两边同时除以b2得到![]() ,再根据题意计算求值即可;
,再根据题意计算求值即可;
(3)利用根与系数的关系结合![]() 求得m的值,根据题意可得
求得m的值,根据题意可得![]() 与
与![]() 是方程
是方程![]() 的两个根,同例题整理得
的两个根,同例题整理得![]() ,得到△ABC为直角三角形,再利用三角形的面积公式求解即可.
,得到△ABC为直角三角形,再利用三角形的面积公式求解即可.
解:(1)由题可知:![]() 与
与![]() 为方程
为方程![]() 的两根,
的两根,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,
显然![]() ,
,
∴![]() ,
,
∴![]()
又∵![]() ,
,
∴![]() ,
,
∴![]() 与
与![]() 为方程
为方程![]() 的两根,
的两根,
∴![]() ;
;
(3)![]()
![]() ,
,
![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∴![]()
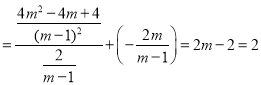 ,
,
∴![]() ,
,
∴![]() 即
即![]() ,
,
![]() 即
即![]() ,
,
∵![]()
∴![]() 与
与![]() 是方程
是方程![]() 的两个根,
的两个根,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 为直角三角形,
为直角三角形,
则![]() .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目