Question

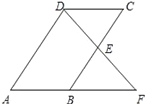
【题目】已知，平行四边形中，连接，，过点作，垂足为，延长与相交于点．

（1）如图1，若，，求线段的长；

（2）如图2，若，过点作于点，连接、．求证：．

Answer 1

【答案】（1）AD＝；（2）见解析

【解析】

（1）根据垂直的定义得到∠AEB＝∠BEC＝90°，根据勾股定理得到BE＝，BC＝，根据平行四边形的性质即可得到结果；
（2）推出△AEB是等腰直角三角形，得到∠ABE＝45°，设∠CBE＝x，根据等腰三角形的性质得到∠ABC＝∠ACB＝45°＋x，求得∠EBC＝22.5°，∠ACB＝67.5°，推出A、B、C、F四点共圆，A、E、F、G四点共圆，得到∠CAF＝∠CBE＝22.5°，∠EGF＝∠EAF＝22.5°，求得∠AGE＝67.5°，推出AE＝GE，根据等腰直角三角形的性质即可得到结论．

（1）解：∵BE⊥AC，
∴∠AEB＝∠BEC＝90°，
∵AE＝2，CE＝1，
∴AC＝AB＝3，
∴BE＝=，
∴BC＝=，
∵四边形ABCD是平行四边形，
∴AD＝BC＝；
（2）证明：∵BE⊥AC，
∴∠AEB＝∠BEC＝90°，
∵∠BAC＝45°，
∴△AEB是等腰直角三角形，
∴∠ABE＝45°，AE＝BE，
∵AB∥CD，
∴∠ACF＝45°，∠ABC＋∠DCB＝180°，
设∠CBE＝x，
∴∠ABC＝45°＋x，
∵AB＝AC，
∴∠ABC＝∠ACB＝45°＋x，
∵∠EBC＋∠ECB＝90°，
∴x＋45°＋x＝90°，
∴x＝22.5°，
∴∠EBC＝22.5°，∠ACB＝67.5°，
∵∠ABF＝∠ACF＝45°，
∴A、B、C、F四点共圆，
∴∠CAF＝∠EBC＝22.5°，
∵FG⊥AD，
∴∠AGF＝∠AEF＝90°，
∴A、E、F、G四点共圆，
∴∠EGF＝∠EAF＝22.5°，
∴∠AGE＝67.5°，
∵∠CAD＝∠ACB＝67.5°，
∴∠EAG＝∠AGE，
∴AE＝GE，
∵AC＝AB＝AE，
∴BE＋EC＝AE＋EC＝AC＝EG．