题目内容
18.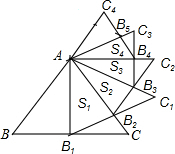 如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)
如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)
分析 由AB1为边长为2的等边三角形ABC的高,利用三线合一得到B1为BC的中点,求出BB1的长,利用勾股定理求出AB1的长,进而求出S1,同理求出S2,依此类推,得到Sn.
解答 解:∵等边三角形ABC的边长为2,AB1⊥BC,
∴BB1=1,AB=2,
根据勾股定理得:AB1=$\sqrt{3}$,
∴S1=$\frac{1}{2}$×$\frac{\sqrt{3}}{4}$×($\sqrt{3}$)2=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)1;
∵等边三角形AB1C1的边长为$\sqrt{3}$,AB2⊥B1C1,
∴B1B2=$\frac{\sqrt{3}}{2}$,AB1=$\sqrt{3}$,
根据勾股定理得:AB2=$\frac{3}{2}$,
∴S2=$\frac{1}{2}$×$\frac{\sqrt{3}}{4}$×($\frac{3}{2}$)2=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)2;
依此类推,Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.
故答案为:$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.
点评 此题考查了等边三角形的性质,属于规律型试题,熟练掌握等边三角形的性质是解本题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
9.今年来某县加大了对教育经费的投入,2013年投入2500万元,2015年投入3500万元.假设该县投入教育经费的年平均增长率为x,根据题意列方程,则下列方程正确的是( )
| A. | 2500x2=3500 | B. | 2500(1+x)2=3500 | ||
| C. | 2500(1+x%)2=3500 | D. | 2500(1+x)+2500(1+x)2=3500 |
6. 如图所示几何体的左视图是( )
如图所示几何体的左视图是( )
 如图所示几何体的左视图是( )
如图所示几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
13.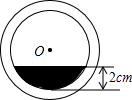 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )| A. | ($\frac{16}{3}$π-4$\sqrt{3}$)cm2 | B. | ($\frac{16}{3}$π-8$\sqrt{3}$)cm2 | C. | ($\frac{8}{3}$π-4$\sqrt{3}$)cm2 | D. | ($\frac{4}{3}$π-2$\sqrt{3}$)cm2 |
3.下列运算正确的是( )
| A. | x2•x3=x6 | B. | (x3)2=x5 | C. | (xy2)3=x3y6 | D. | x6÷x3=x2 |
7. 如图,下列条件不能判定△ADB∽△ABC的是( )
如图,下列条件不能判定△ADB∽△ABC的是( )
 如图,下列条件不能判定△ADB∽△ABC的是( )
如图,下列条件不能判定△ADB∽△ABC的是( )| A. | ∠ABD=∠ACB | B. | ∠ADB=∠ABC | C. | AB2=AD•AC | D. | $\frac{AD}{AB}$=$\frac{AB}{BC}$ |
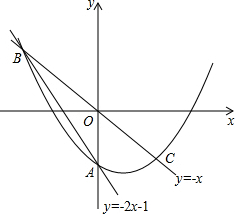 在平面直角坐标系中,O为原点,直线y=-2x-1与y轴交于点A,与直线y=-x交于点B,点B关于原点的对称点为点C.
在平面直角坐标系中,O为原点,直线y=-2x-1与y轴交于点A,与直线y=-x交于点B,点B关于原点的对称点为点C.