题目内容
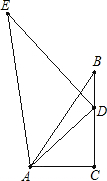如图，∠ADE=∠ACB=90°，∠AED=∠ABC，若AE=5，ED=4，AB=3，求BC的长．
分析：由题中可知△ADE∽△ACB，进而利用相似三角形对应边成比例，求解线段的长．
解答：解：∵∠ADE=∠ACB=90°，∠AED=∠ABC
∴△ADE∽△ACB（2分）
∴
=
．（3分）
∵AE=5，ED=4，AB=3，
∴BC=
．（5分）
∴△ADE∽△ACB（2分）
∴
| AE |
| AB |
| ED |
| BC |
∵AE=5，ED=4，AB=3，
∴BC=
| 12 |
| 5 |
点评：本题主要考查了相似三角形的判定及性质．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
1、如图，∠ADE和∠CED是（ ）
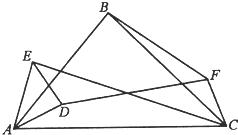30、如图，△ADE和△ABC中∠EAD=∠AED=∠BAC=∠BCA=45°，又有∠BAD=∠BCF．（1）求∠ECF+DAC+∠ECA的度数；
（2）判断ED与FC的位置关系，并对你的结论加以证明．
8、如图，△ADE∽△ABC，若AD=1，BD=2，则△ADE与△ABC的相似比是（ ）
如图，△ADE的顶点D在△ABC的BC边上，且AD=AB，BC=DE，∠B=∠ADE，则下列结论不正确的是（ ）| A、∠C=∠E | B、∠B=∠ADC | C、∠BAD=∠CAE | D、∠CDE=∠CAE |
如图，∠ADE=∠AED=2∠B=2∠C，则图中共有等腰三角形个数为（ ）