题目内容
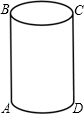 如图,圆柱高12cm,底面半径为3cm.圆柱下底面A点的蚂蚁,想沿圆柱的侧面爬行,吃到上底面上与A点相对的C点处的食物,需爬行的最短路程是________cm.(π取3)
如图,圆柱高12cm,底面半径为3cm.圆柱下底面A点的蚂蚁,想沿圆柱的侧面爬行,吃到上底面上与A点相对的C点处的食物,需爬行的最短路程是________cm.(π取3)
15
分析:首先画出圆柱的平面展开图,求出CB长,再利用勾股定理可求出AB的长.
解答: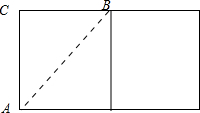 解:连接AB,
解:连接AB,
由题意得:CB= ×2π×3=3π≈9(cm),
×2π×3=3π≈9(cm),
AC=12cm,
则AB= =15(cm).
=15(cm).
故答案为:15.
点评:此题主要考查了平面展开-最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.
分析:首先画出圆柱的平面展开图,求出CB长,再利用勾股定理可求出AB的长.
解答:
 解:连接AB,
解:连接AB,由题意得:CB=
 ×2π×3=3π≈9(cm),
×2π×3=3π≈9(cm),AC=12cm,
则AB=
 =15(cm).
=15(cm).故答案为:15.
点评:此题主要考查了平面展开-最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.

练习册系列答案
相关题目
 如图,圆柱的底面周长为12cm,AC是底面圆的直径,高BC=10cm,点P是BC上一点且PC=
如图,圆柱的底面周长为12cm,AC是底面圆的直径,高BC=10cm,点P是BC上一点且PC=| 4 |
| 5 |
| A、9cm | B、10cm |
| C、11cm | D、12cm |
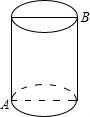 如图,圆柱的高为12cm,底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离是多少cm?(π取3).
如图,圆柱的高为12cm,底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离是多少cm?(π取3). 如图,圆柱高12cm,底面半径为3cm.圆柱下底面A点的蚂蚁,想沿圆柱的侧面爬行,吃到上底面上与A点相对的C点处的食物,需爬行的最短路程是
如图,圆柱高12cm,底面半径为3cm.圆柱下底面A点的蚂蚁,想沿圆柱的侧面爬行,吃到上底面上与A点相对的C点处的食物,需爬行的最短路程是