题目内容
等腰三角形一腰上的高与另一腰的夹角为45°，则其顶角为（ ）
| A、45° |
| B、135° |
| C、45°或67.5° |
| D、45°或135° |
考点：等腰三角形的性质
专题：
分析：首先根据题意画出图形，一种情况等腰三角形为锐角三角形，即可推出顶角的度数为45°．另一种情况等腰三角形为钝角三角形，由题意，即可推出顶角的度数为135°．
解答：
解：①如图，等腰三角形为锐角三角形，
∵BD⊥AC，∠ABD=45°，
∴∠A=45°，
即顶角的度数为45°．
②如图，等腰三角形为钝角三角形，
∵BD⊥AC，∠DBA=45°，
∴∠BAD=45°，
∴∠BAC=135°．
故选D．
解：①如图，等腰三角形为锐角三角形，∵BD⊥AC，∠ABD=45°，
∴∠A=45°，
即顶角的度数为45°．
②如图，等腰三角形为钝角三角形，
∵BD⊥AC，∠DBA=45°，
∴∠BAD=45°，
∴∠BAC=135°．
故选D．
点评：本题主要考查了直角三角形的性质、等腰三角形的性质．此题难度适中，解题的关键在于正确的画出图形，结合图形，利用数形结合思想求解．
练习册系列答案
相关题目
10名同学分成甲、乙两队进行篮球比赛，他们的身高（单位：cm）如下表所示：
设两队队员身高的平均数依次为
甲，
乙，身高的方差依次为S2甲，S2乙，则下列关系中完全正确的是（ ）
| 队员1 | 队员2 | 队员3 | 队员4 | 队员5 | |
| 甲队 | 173 | 175 | 175 | 175 | 177 |
| 乙队 | 170 | 171 | 175 | 179 | 180 |
. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在等边三角形ABC中，AB=2，AD平分∠BAC，交BC于点D，DE⊥AB于点E，DF⊥AC于点F，则下列说法错误的是（ ）| A、DE=DF | ||||
| B、∠BDE=∠CDF=30° | ||||
C、AD=
| ||||
D、S△BDE=
|
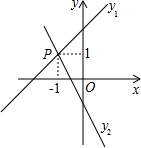如图，已知直线y1=x+m与y2=kx-1相交于点P（-1，1），关于x的不等式x+m＞kx-1的解集是（ ）| A、x≥-1 | B、x＞-1 |
| C、x≤-1 | D、x＜-1 |
已知a，b两数在数轴上的位置如图，则化简代数式|b-a|+|a+b|-|a+2b|的结果是（ ）| A、3a+2b | B、2b+3 |
| C、2a-3 | D、-1 |
若
=
，则
等于（ ）
| x |
| y |
| 2 |
| 7 |
| 7x2-3xy+2y2 |
| 2x2-3xy+7y2 |
A、
| ||
B、
| ||
| C、7 | ||
| D、1 |