题目内容
一块直角三角形的木板，三边长分别是3m，4m和5m，要把它加工成面积最大的正方形桌面，甲、乙两同学的设计方案如图所示，请你用学过的知识说明哪名同学的设计方案符合要求．分析：图1中，△AFD∽△ACB，求出FD，即得出正方形的边长；图2中，过点C作CM⊥AB于点M，求出CM的长度，再由平行线分线段成比例的性质，可得出正方形的边长，比较即可得出答案．
解答：解：图1中，∵△AFD∽△ACB，
∴
=
，即
=
，
解得：FD=
；
图2中，过点C作CM⊥AB于点M，如图所示：
CM=
=
，设正方形的边长为x，
∵GF∥AB，
∴
=
，即
=
，
解得：x=
，
∵
＞
，
∴甲同学的设计方案符合要求．
∴
| FD |
| BC |
| AF |
| AC |
| FD |
| 3 |
| 4-FD |
| 4 |
解得：FD=
| 12 |
| 7 |
图2中，过点C作CM⊥AB于点M，如图所示：
CM=
| AC×BC |
| AB |
| 12 |
| 5 |
∵GF∥AB，
∴
| CN |
| CM |
| GF |
| AB |
| x |
| 5 |
| ||
|
解得：x=
| 60 |
| 37 |
∵
| 12 |
| 7 |
| 60 |
| 37 |
∴甲同学的设计方案符合要求．
点评：此题考查了相似三角形的性质，相似三角形的对应边成比例；相似三角形的对应高的比等于相似比；解此题的关键是将实际问题转化为数学问题进行解答．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
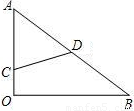
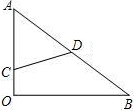如图，有一块直角三角形的木板AOB，∠O=90°，OA=3，OB=4，一只小蚂蚁在OA边上爬行（可以与O、A重合），设其所处的位置C到AB的中点D的距离为x，则x的取值范围是
一块直角三角形的木板，三边长分别是3m，4m和5m，要把它加工成面积最大的正方形桌面，甲、乙两同学的设计方案如图所示，请你用学过的知识说明哪名同学的设计方案符合要求．