Question

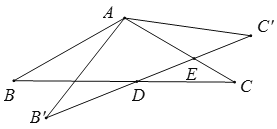
【题目】如图，在矩形中，，，，分别是边、上任意点.以线段为边，在上方作等边，取边的中点，连接，则的最小值是_______．

Answer 1

【答案】

【解析】

先证明点F、B、E、H四点共圆，进而可得∠FBH=∠FEH=60°，再根据，求得tan∠ABD=，进而可得∠ABD=60°，由此可得点B、H、D在同一直线上，则当CH⊥BD时，CH取得最小值，最后根据等积法求得CH的最小值即可．

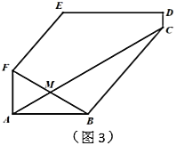
解：如图，连接FH，BH，BD，

∵在矩形ABCD中，

∴∠FBE=∠A=∠BCD=90°，，，

∴在Rt△BCD中，，

∵在等边中，点H为EG的中点，

∴FH⊥GE，∠FEH=60°，

∴∠FHE=90°，

又∵∠FBE=90°，

∴点F、B、E、H四点共圆，

∴∠FBH=∠FEH=60°，

∵在Rt△ABD中，，，

∴tan∠ABD=，

∴∠ABD=60°，

∴点B、H、D在同一直线上，

∴当CH⊥BD时，CH取得最小值，

若CH⊥BD，则

∴，

∴CH的最小值为，

故答案为：