题目内容
 如图,CD平分∠ACB,DE∥BC,∠AED=80°
如图,CD平分∠ACB,DE∥BC,∠AED=80°(1)求∠EDC的度数;
(2)请你画出△BDC的中线BF,再画出BF的中点G,连接DG.若S△BCD=30,求△BDG的面积.
考点:三角形的面积,平行线的性质
专题:
分析:(1)根据平行线的性质求出∠ACB,根据角平分线定义求出即可;
(2)如图,根据中点的确定方法找到中线.由“三角形的中线把三角形分成面积相等的两部分”进行解答.
(2)如图,根据中点的确定方法找到中线.由“三角形的中线把三角形分成面积相等的两部分”进行解答.
解答: 解:(1)∵DE∥BC,∠AED=80°,
解:(1)∵DE∥BC,∠AED=80°,
∴∠ACB=∠AED=80°,
∵CD平分∠ACB,
∴∠ECD=
∠ACB=40°;
(2)BF、DG如图所示.
∵BF是CD边上的中线,S△BCD=30,
∴S△BDF=
S△BCD=15.
又DG是BF边上的中线,
∴S△BDG=
S△BCD=7.5.
 解:(1)∵DE∥BC,∠AED=80°,
解:(1)∵DE∥BC,∠AED=80°,∴∠ACB=∠AED=80°,
∵CD平分∠ACB,
∴∠ECD=
| 1 |
| 2 |
(2)BF、DG如图所示.
∵BF是CD边上的中线,S△BCD=30,
∴S△BDF=
| 1 |
| 2 |
又DG是BF边上的中线,
∴S△BDG=
| 1 |
| 2 |
点评:本题考查了平行线的性质和角平分线定义的应用,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,题目比较好,难度适中.

练习册系列答案
相关题目
下列根式中,与
是同类二次根式的是( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知△ABC中,∠ABC为钝角.请你按要求作图(不写作法,但要保留作图痕迹):
已知△ABC中,∠ABC为钝角.请你按要求作图(不写作法,但要保留作图痕迹):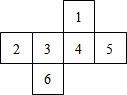 如图是正方体的一种展开图,其中每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是
如图是正方体的一种展开图,其中每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是