题目内容
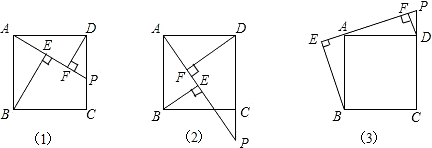
 如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP.
如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP.(1)当m=3时,求点A的坐标及BC的长;
(2)当m>1时,连结CA,问m为何值时CA⊥CP.
考点:二次函数综合题
专题:
分析:(1)首先令y=0,求出A点坐标,进而得出B点坐标,进而求出BC的长;
(2)过点C作CH⊥x轴于点H,连接AC,得出△ACH∽△PCB,进而求出AH=1,CH=2m-1,进而得出m的值.
(2)过点C作CH⊥x轴于点H,连接AC,得出△ACH∽△PCB,进而求出AH=1,CH=2m-1,进而得出m的值.
解答:解:(1)当m=3时,y=-x2+6x令y=0,
得-x2+6x=0,
解得:x1=0,x2=6,
则A(6,0)
当x=1时,y=5,故B(1,5)
∵抛物线y=-x2+6x的对称轴为直线x=3,
又∵B、C关于对称轴对称,
∴BC=4;
(2)过点C作CH⊥x轴于点H,
由已知得∠ACP=∠BCH=90°
∴∠ACH=∠PCB
又∵∠AHC=∠PBC=90°,
∴△ACH∽△PCB
∴
=
,
∵抛物线y=-x2+2mx(m>0)的
对称轴为直线x=m,其中m>1,
又∵B,C关于对称轴对称,
∴BC=2(m-1)
∵B(1,2 m-1),P(1,m),
∴BP=m-1,
又∵A(2m,0),C(2m-1,2m-1),
∴H(2m-1,0)
∴AH=1,CH=2m-1
∴
=
,
解得:m=
,
即m=
时CA⊥CP.
得-x2+6x=0,
解得:x1=0,x2=6,

则A(6,0)
当x=1时,y=5,故B(1,5)
∵抛物线y=-x2+6x的对称轴为直线x=3,
又∵B、C关于对称轴对称,
∴BC=4;
(2)过点C作CH⊥x轴于点H,
由已知得∠ACP=∠BCH=90°
∴∠ACH=∠PCB
又∵∠AHC=∠PBC=90°,
∴△ACH∽△PCB
∴
| AH |
| CH |
| PB |
| PC |
∵抛物线y=-x2+2mx(m>0)的
对称轴为直线x=m,其中m>1,
又∵B,C关于对称轴对称,
∴BC=2(m-1)
∵B(1,2 m-1),P(1,m),
∴BP=m-1,
又∵A(2m,0),C(2m-1,2m-1),
∴H(2m-1,0)
∴AH=1,CH=2m-1
∴
| 1 |
| 2m-1 |
| m-1 |
| 2(m-1) |
解得:m=
| 3 |
| 2 |
即m=
| 3 |
| 2 |
点评:此题主要考查了二次函数综合以及相似三角形的判定与性质等知识,利用m表示出各边长是解题关键.

练习册系列答案
相关题目
若函数y=k(3-x)与y=
在同一坐标系内的图象相交,其中k<0,则交点在( )
| k |
| x |
| A、第一、三象限 |
| B、第四象限 |
| C、第二、四象限 |
| D、第二象限 |
不等式组
的解集在数轴上表示为( )
|
A、 |
B、 |
C、 |
D、 |
 如图,△ABC中,AE是高,AD是角平分线.∠B=46°,∠C=60°,求∠DAE的度数.
如图,△ABC中,AE是高,AD是角平分线.∠B=46°,∠C=60°,求∠DAE的度数. 已知四边形ABCD是边长为4
已知四边形ABCD是边长为4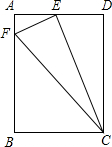 如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC(AB>AE).
如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC(AB>AE).