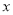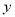题目内容
如图,CA为⊙O的切线,切点为A,点B在⊙O上,若∠CAB=55°,则∠AOB等于( )

A. 55° B. 90° C. 110° D. 120°
C 【解析】因为CA为⊙O的切线,所以OA⊥AC,所以∠OAC=90°. 因为∠CAB=55°,所以∠OAB=90°-55°=35°, 因为OA=OB,所以∠OAB=∠B. 所以∠AOB=180°-2×35°=110°. 故选C.
练习册系列答案
相关题目
已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
| … |
| 0 | 1 | 3 | … |
| … |
| 1 | 3 | 1 | … |
则下列判断中正确的是( )
A. 抛物线开口向上 B. 抛物线与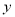 轴交于负半轴
轴交于负半轴
C. 当x=4时,y>0 D. 方程ax2+bx+c=0的正根在3与4之间
D 【解析】试题分析:如果将已知任意三点代入y=ax2+bx+c中求解,那么计算量较大,而由表格知,当x=0和x=3时y=1,故抛物线对称轴为直线,结合已知点可画y=ax2+bx+c的草图(如图所示),根据图象知A、B、C错.故选D.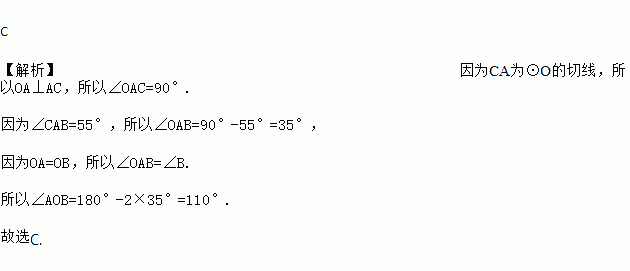

 B.
B. 
 D.
D. 
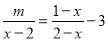 有增根,则实数m的值是_______.
有增根,则实数m的值是_______.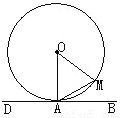
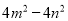 的值;
的值;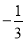 ,y =3.
,y =3.