题目内容
若用半径为9，圆心角为120°的扇形围成一个圆锥的侧面，接缝忽略不计，则这个圆锥的底面半径是________．
3
分析：根据图形可知，圆锥的侧面展开图为扇形，且其弧长等于圆锥底面圆的周长．
解答：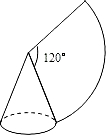
解：设这个圆锥的底面半径是R，则有：
2πR=120π×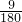
，
解得：R=3．
故答案为：3．
点评：此题考查了圆锥侧面展开扇形与底面圆之间的关系，圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把的扇形的弧长等于圆锥底面周长作为相等关系，列方程求解．
分析：根据图形可知，圆锥的侧面展开图为扇形，且其弧长等于圆锥底面圆的周长．
解答：
解：设这个圆锥的底面半径是R，则有：2πR=120π×
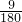，解得：R=3．
故答案为：3．
点评：此题考查了圆锥侧面展开扇形与底面圆之间的关系，圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把的扇形的弧长等于圆锥底面周长作为相等关系，列方程求解．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
若用半径为9，圆心角为120°的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的底面半径是（ ）| A、1.5 | B、2 | C、3 | D、6 |
若用半径为9，圆心角为120°的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的底面半径是
若用半径为12，圆心角为120°的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥底面圆的半径的长