题目内容
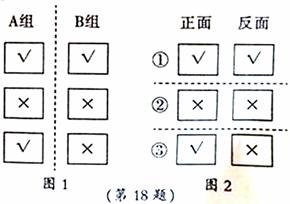
有六张完全相同的卡片,分A、B两组,每组三张,在A组的卡片上分别画上“√、×、√”,B组的卡片上分别画上“√、×、×”,如图1所示。
(1)若将卡片无标记的一面朝上摆在桌上,再发布从两组卡片中随机各抽取一张,求两张卡片上标记都是√的概率(请用树形图法或列表法求解)
(2)若把A、B两组卡片无标记的一面对应粘贴在一起得到3张卡片,其正反面标记如图2所示,将卡片正面朝上摆放在桌上,并用瓶盖盖住标记。
①若随机揭开其中一个盖子,看到的标记是√的概率是多少
②若揭开盖子,看到的卡片正面标记是√后,猜想它的反面也是√,求猜对的概率。
(1)解法一:
根据题意,可画出如下树形图:
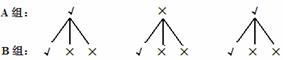
从树形图可以看出,所有可能结果共有9种,且每种结果出现的可能性都相等,其中两张卡片上标记都是“√”的结果有2种。
∴P(两张都是“√”)=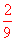 .
.
解法二:
根据题意,可列表如下:

从上表中可以看出,所有可能结果共有9种,且每种结果出现的可能性都相等,其中两张卡片上标记都是“√”的结果有2种。
(2)
①∵根据题意,三张卡片正面的标记有三种可能,分别为“√”、“×”、“√”,
∴随机揭开其中一个盖子,看到的标记是“√”的概率为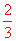 .
.
②∵正面标记为为“√”的卡片,它的反面标记只有两种情况,分别为“√”和“×”,
∴猜对反面也是“√”的概率为P=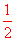 .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目