题目内容
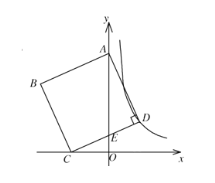
【题目】如图，在平面直角坐标系中，正方形ABCD的面积为20，顶点A在y轴上，顶点C在x轴上，顶点D在双曲线
的图象上，边CD交y轴于点E，若
，则k的值为______.
【答案】4
【解析】
过D作DF⊥x轴并延长FD，过A作AG⊥DF于点G，利用正方形的性质易证△ADG≌△DCF，得到AG=DF，设D点横坐标为m，则OF=AG=DF=m，易得OE为△CDF的中位线，进而得到OF=OC，然后利用勾股定理建立方程求出
，进而求出k.
如图，过D作DF⊥x轴并延长FD，过A作AG⊥DF于点G，
∵四边形ABCD为正方形，
∴CD=AD，∠ADC=90°
∴∠ADG+∠CDF=90°
又∵∠DCF+∠CDF=90°
∴∠ADG=∠DCF
在△ADG和△DCF中，
∵∠AGD=∠DFC=90°，∠ADG=∠DCF，AD=CD
∴△ADG≌△DCF（AAS）
∴AG=DF
设D点横坐标为m，则OF=AG=DF=m，
∴D点坐标为(m,m)
∵OE∥DF，CE=ED
∴OE为△CDF的中位线，
∴OF=OC
∴CF=2m
在Rt△CDF中，
∴
解得
又∵D点坐标为(m,m)
∴
故答案为：4.
练习册系列答案
相关题目
